Knights Moving
Problem

Two white and two black knights are positioned on part of a chess board as shown.
A knight can only move in the usual way * and can only land on an empty square.
Swap the positions of the white and black knights.
Can you prove you have succeeded in the minimum number of moves?
* A knight can move two squares horizontally and one square vertically, or two squares vertically and one square horizontally. The complete move therefore looks like the letter 'L'.
Unlike all other standard chess pieces, the knight can 'jump over' all other pieces on route to its destination square.
Getting Started
Where can you move first?
What are the possibilities for your second move?
What for the third?
...
Think about how a counter can move around the board.
Some squares offer you less choice. Is this significant?
Is there another way you can visualise this problem?
How will you record what you have done?
Student Solutions
While it may be tempting, and fun, to simply try to do the puzzle as it for a while, there is a rather nice way of simplifying the problem.
By joining up each of the squares that are connected by a knights move, we can reduce the problem down to a graph, where the knights can move along connected nodes.
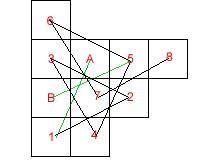
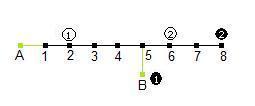
The graph turns out to be rather simple! All of the squares end up on a single line, with the single square 'B' branching off.
Clearly, by moving the pieces along one node at a time, the only place where any swapping can happen is at B. The quickest way would be to swap W1 and B1 , and swap W2 and B2 (otherwise there would be even more swapping. There are two ways of doing this:
Swapping W1 and B1, then W2 and B2:
- W2: 6 to 7
- W1: 2 to 6
- B1: B to 2
- W1: 6 to 3 (we've now swapped W1 and B1, making room for the next swap)
- W2: 7 to B
- B2: 8 to 4
- W2: B to 8
- B2: 4 to 6.
- W1: 3 to B. Done! 28 moves
Swapping W2 and B2, then W1 and B1:
- B1: B to 3
- W2: 6 to B
- B2: 8 to 4
- W2: B to 8
- B2: 4 to 7 (we've swapped W2 and B2, making room for the next swap)
- B1: 3 to 6
- W1: 2 to B
- B1: 6 to 2 (we've now swapped W1 and B1)
- B2: 7 to 6. Done! 28 moves
So the minimum number of moves is 28.
Teachers' Resources
This is the sort of problem that needs a lot of thinking time.
Present it and leave it for a week or so before returning to it ...
If no one has made much progress - what have they managed to do?
At some stage it may be worth mentioning that the solution requires more than 20 moves.
What recording methods have people come up with?
Then the big question:
How can you know you have managed to swap the knights in the minimum number of moves? This will certainly need a convincing recording system.
