How Does Your Function Grow?
Compares the size of functions f(n) for large values of n.
Problem
Four enthusiastic mathematicians are asked to think of a function involving the number 100. The challenge is to think of the function which is biggest for big values of n
- Archimedes chooses a logarithm function $$A(n) = \log(100n)$$
- Bernoulli decides to take 100th powers $$B(n) = n^{100}$$
- Copernicus takes powers of 100 $$C(n) = 100^n$$
- and, finally, de Moivre, who likes to be different, chooses the
factorial function which he claims will be quite big enough without
any reference to 100 at all $$D(n) = n\times (n-1)\times
(n-2)\times \dots \times 2\times 1$$
Which function is biggest for large values of n? Can you determine a value beyond which you know this function will be biggest?[Extension: To find the exact switch-over value will be difficult and will require the clever use of a spreadsheet or computer.]What could you say if the 100s were replaced by a million? billions? Create a convincing argument to prove your results to the mathematicians.
Getting Started
Think about the meaning of each of the functions carefully. Try writing them out in full, explicit notation and comparing them. The log function is somewhat different in definition to the other three, but you can look at the effect of log on the other functions to develop a sense for its speed of growth.
Student Solutions
Here are two solutions, one from Simon from Elizabeth College, Guernsey and one from Andrei from Tudor Vianu National College, Bucharest, Romania. First Simon's solution.
The functions are: $$\eqalign { A(n) &= \log(100n) \cr B(n) &= n^{100} \cr C(n) &= 100^n \cr D(n) &= n! .}$$ Firstly I looked at Archimedes' choice, the logarithmic function. $$A(n) = \log(100n) = \log 100 + \log n.$$ I knew that when $n$ gets large $\log 100$ would become irrelevant. This meant that only $\log n$ would be important, and $\log n < n$ when $n > 1$. So $A(n)$ will be less than $n$ for large $n$. We find $n = \log(100)+ \log n$ for $n = 6.472775$ approximately and so $A(n) < n$ for all values of $n> 6.5$.\par The next task was establish whether $B(n)$ or $C(n)$ was greater for large numbers. I was certain of one thing: $B(n) = C(n) = 100^{100}$ for $n=100$.
Firstly I knew that $100^n$ would have $2n+1$ digits. I then established, where $x$ is the number of digits in $n$, that $n^{100}$ would have between $100(x-1)+1$ and $100x$ digits. So $C(n) = 100^n$ is the larger function for $n> 100$.
Therefore, so far, $C(n)$ is the largest function for large values of $n$.
The next task was to compare it to $D(n)$ or factorial $n$.
Using Stirling's formula: $$D(n) = n! = \sqrt{2\pi n} ({n\over e})^n.$$ As $n$ is a large positive number, $\sqrt {2\pi n}$ will be greater than 1. Therefore when ${n\over e}$ is greater than 100, $D(n) > C(n)$. The 'change over point' occurs for $n$ just less than $n = 100e$, that is $ n \approx 270$.
Andrei considered the natural logarithms of the functions and plotted their graphs. For the factorial n function Andrei used Stirling's Approximation which is valid for large n.
I approximated the function for factorial n further by
ignoring the term $\sqrt{2\pi n}$. $$\eqalign{ A(x)&= \log (n)
+ \log(100) \cr \log(B(n)) &= 100 \log(n)\cr \log C(n) &= n
\log(100) \cr \log D(n)&\approx n\log(n) - n }.$$ I know that
$log(n)< n$ for the whole domain of definition of the
logarithmic function, and I see that $A$ is the smallest. I have to
compare the other functions. As $ \log(100)\approx 4.60$, so:
$$\eqalign { \log(B) &= 100 \log(n) \cr \log(C)&\approx
4.6n \cr \log(D) &\approx n (\log(n) -1).}$$ In the limit for
large $n$, $$ \lim_{n\to \infty}{\log n\over n}\to 0$$ and so
$B< C$.
For large $n$ we can neglect 1 in respect to $\log(n)$ in the
approximate formula for $\log(D)$ and, as $4.6 < \log (n)$ we
have $D> C> B> A$.
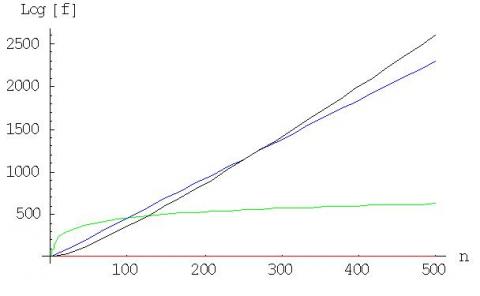
Here in the diagram, $A(x)$ is represented in red, $B(x)$ in
green, $C(x)$ in blue and $D(x)$ in black. It can be observed that
for large $n$ (here $n> 300$) the order of the magnitude of the
functions is $D> C> B> A$.
Image
Teachers' Resources
For many applications mathematicians are not concerned about the exact numerical values of functions but, rather, their behaviour for large values of the variable. Why? One important reason is in the generation of algorithms for implementation on computers: it is often possible to relate the time that the algorithm will take to complete in terms of a simple mathematical function of the number of variables going into the algorithm. Algorithms which take too long to complete will be practically useless, although they may be theoretically beautiful.
An example is the following test, discovered in the 18th century by John Wilson, to see if a number is prime or not:
p is a prime number if and only if (p-2)! = 1mod p
Try using this and you will discover that it is highly inefficient as a way of actually testing for primality, although it is a very beautiful result mathematically.
