Dotty Circle
Problem
Watch the film below.
Try to describe what happens in the film to someone else.
Imagine the dot starts at the point (1,0), turns through $20^\circ$ and then stops: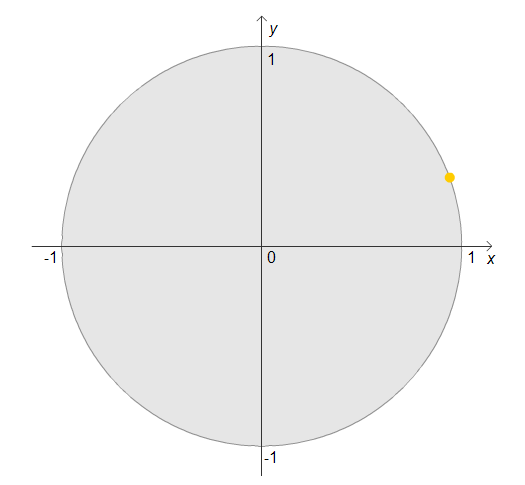
If the point now carries on, through how many degrees must it turn to finish the same height above or below the horizontal axis as it was when it had gone through $20^\circ$?
Can you find a general rule for explaining when the dot will be this same distance from the horizontal axis?
You might like to try Round and Round and Round after this problem.
Getting Started
Why not watch the film again and concentrate on the distance from the spot to the horizontal axis?
Is there only one answer?
It might help to draw some sketches of your own.
Student Solutions
Pupils from Stradbroke Primary School sent in some well-thought out solutions to this problem. Roni explains how they worked out how much further (from $20^\circ$) the point would have to turn to finish the same height above or below the horizontal axis:
1. A whole circle is $360^\circ$, half a circle is $180^\circ$.$180^\circ$ take away $20^\circ$ and then take away another $20^\circ$ gives the answer of $140^\circ$.
2. The first $20^\circ$ is above the x line and the third $20^\circ$ is under the x line so it's always $180^\circ$.
3. A whole circle is $360^\circ$, you take away $20^\circ$ and then another $20^\circ$. 20 add 20 equals 40. 360 take away 40 equals $320^\circ$.
So, Roni has concluded that there are three other points where the dot would be the same distance from the horizontal axis as it is for $20^\circ$. Another way of looking at it would be to say that the dot itself would have to be at $20^\circ$, $160^\circ$, $200^\circ$and $340^\circ$.
George tells us how we can work out how far a point at any position on the circle would have to turn to finish the same height above or below the horizontal axis. He agrees that there will be three other solutions:
1. Double the first degree and take it away from $180^\circ$.
2. Add $180^\circ$ to the your starting degree.
3. Double the starting degree and take it away from $360^\circ$.
Well done!
Teachers' Resources
The following is an extract from the notes provided by Alf Coles on his site, which was the insipration for this problem:
"I am aware of wanting to create a sense of drama and performance before showing a film. I make myself as still as I can and offer a minimum of context save that the task, having watched the film, will be to try and re-create together what we saw. However, students should not worry about trying to remember it, but just be present in what they see.
As the film finishes I am again aware of wanting to make myself as still as possible, pausing for as long as possible and speaking as slowly as I can. 'We are now going to try and re-construct what we saw. We will all have lots of images in our heads and images will be sparked off by what others say. Before we start sharing these images, there is one rule. When someone is talking your task is to
try and see what they say and, as much as you can, to let go of your own images in order to do that ... Okay, could someone offer us an image from the very beginning of the film. What did you see?'
One rule I give myself is not to speak second. With many groups the second speaker will not make a comment related to the first. If this happens I will remind the group of the rule and invite a comment about what the first speaker said.
I am not sure it is possible to say much more about working with film (and I have possibly said too much already) except to try it out!"
This particular problem is a great context in which to generalise and by that, we do not necessarily mean the use of algebraic expressions at this level. Encourage pupils to put into words the symmetry that they see, using what they know about the number of degrees in a circle - this is an equally valid way to generalise.
This activity is great for laying foundations for trigonometry, even though this is a topic which pupils will not officially meet until much later. To extend the ideas in this problem, your class could try A Quarter of a Million Degrees .
