Pythagoras on a Sphere
Prove Pythagoras' Theorem for right-angled spherical triangles.
Problem
Image
|
You only need elementary
trigonometry and scalar products
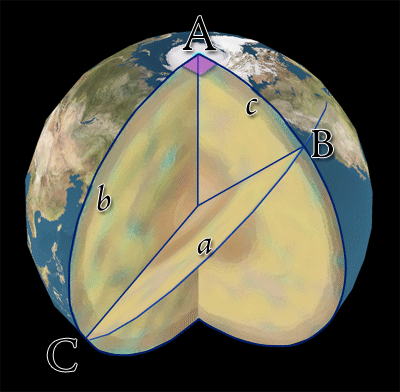
Given any right-angled triangle $\Delta ABC$ on a sphere of
unit radius, right angled at $A$, and with lengths of sides $a, b$
and $c$, then Pythagoras' Theorem in Spherical Geometry is $$\cos a
= \cos b \cos c.$$ Prove this result.
Find a triangle containing three right angles on the surface
of a sphere of unit radius. What are the lengths of the sides of
your triangle?
Use the Pythagoras' Theorem result above to prove that all
spherical triangles with three right angles on the unit sphere are
congruent to the one you found.
|
Getting Started
|
All angles are in radians.
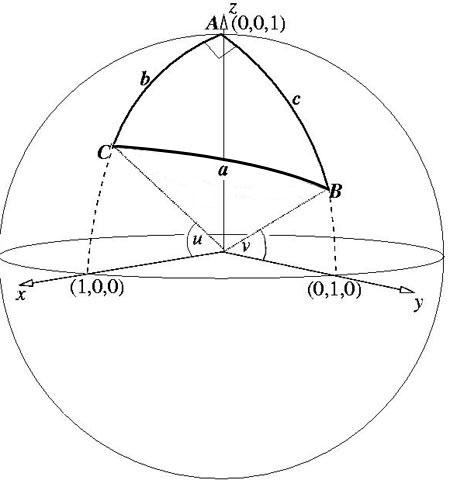
(1) Without loss of generality take coordinate axes so that
$A$ is the point$(0,0,1)$, the xz-plane contains the point $C$ and
the yz-plane contains the point $B$.
(2) Thinking of $A$ as the North Pole then $C$ has latitude
$u$ and longitude 0 and $B$ has latitude $v$ and longitude
$\pi/2$.
(3) Find the 3D coordinates of $B$ and $C$. Where the origin O
is the centre of the sphere ${\bf OA, OB}$ and ${\bf OC}$ are
vectors of unit length.
(4) Use scalar products and vectors ${\bf OA, OB}$ and ${\bf
OC}$ to find the lengths of the arcs $AB, BC$ and $CA$ in terms of
$u$ and $v$. The required result follows.
|
Image
|
Student Solutions
Image

|
Many thanks Andrei from Tudor Vianu
National College, Bucharest, Romania for another excellent
solution.
To solve the problem I have used the hint, so that all
notations are from the hint. I have associated to the sphere a
system of Cartesian coordinates, as shown in the sketch.
Without loss of generality, I have assumed that $A$ is
situated on $Oz$, and has coordinates (0, 0, 1). As $A$ is a right
angle, I can assume that $B$ is situated in the plane $yOz$ and $C$
in plane $xOz$ respectively.
Let the angle $xOC$ be $u$, and angle $yOB$ be $v$. So, the
Cartesian coordinates of the three points, which correspond to the
vectors OA, OB and
OC , are: $$A(0, 0, 1),\
B(0, \cos v, \sin v),\ C(\cos u, 0, \sin u).$$
|
Arcs $AB, BC$ and $CA$ are arcs on the three great circles (of
radius unity), so that their lengths are equal to the angles at the
centre in the corresponding great circle (expressed in radians).
So, as shown in the figure: $$\angle BOC = a,\ \angle AOC = b =
{\pi \over 2} - u, \ \angle AOB = c = {\pi \over 2} - v. \quad
(1)$$ To calculate the length of arc $BC$ I use the same procedure
as in the problem "Flight path". I calculate first the straight
line distance between $B$ and $C$ inside the Earth: $$BC^2 = \cos^2
u + \cos^2 v + \sin^2 u + \sin^2 v - 2\sin u \sin v = 2 (1 - \sin u
\sin v). \quad (2)$$ But from (1) I observe that $\sin u = \cos b$
and $\sin v = \cos c$. Using these and (2), I obtain $BC^2$: $$BC^2
= 2 (1 - \cos b \cos c). \quad (3)$$ Applying the cosine theorem in
triangle $BOC$, I shall obtain the measure of $\angle BOC$, which
is given by: $$BC^2 = BO^2 + CO^2 - 2 BO\times CO \cos a = 2(1 -
\cos a). \quad (4)$$ From (3) and (4) we get Pythagoras' Theorem on
the sphere: $$\cos a = \cos b \cos c.$$ An alternative proof of
Pythagoras' Theorem on the sphere uses scalar products as
follows.
Since ${\bf OA, OB}$ and ${\bf OC}$ are unit vectors, the
angles between the vectors, and hence the lengths of the sides of
triangle $ABC$, are given from the scalar products: $$\eqalign{ a
&=\cos^{-1}{\bf OB.OC}= \cos^{-1}\sin u \sin v\cr b &=
\cos^{-1}{\bf OA.OC}= \cos^{-1}\sin v\cr c &= \cos^{-1}{\bf
OB.OA}= \cos^{-1}\sin u.}$$ Hence $$\cos a = \cos b \cos c.$$ For
the second part of the problem I observe that the triangle with
vertex coordinates (0, 0, 1), (0, 1, 0) and (1, 0, 0) has 3 right
angles. The lengths of its sides are all $\pi/2$. Now I shall prove
that all spherical triangles with 3 right angles are equilateral of
side $\pi/2$. All the following relations follow from the version
of Pythagoras Theorem proved above as angles $A = B = C = \pi/2$.
\begin{eqnarray} \cos a &= \cos b \cos c. \quad (5)\\ \cos b
&= \cos c \cos a. \quad (6)\\ \cos c &= \cos a \cos b.
\quad (7)\\ \end{eqnarray} Multiplying (5), (6) and (7), I obtain:
$$\cos a \cos b \cos c = (\cos a \cos b \cos c)^2.$$ If $\cos a,
\cos b, \cos c \neq 0$, then $\cos a \cos b \cos c = 1$. But $-1
\leq \cos a, \cos b, \cos c \leq 1.$ So, $\cos a= \cos b = \cos c =
1$, which means $a = b = c = 0$ (impossible) or $\cos a = \cos b =
-1$ and $\cos c = 1$ (or any other combination of $a, b$ and $c$),
which is also impossible.
So, one of $\cos a, \cos b$ or $\cos c$ is 0. Now, evidently
$\cos a = \cos b = \cos c = 0$, so $a = b = c = \pi /2$, and all
triangles with this property are congruent.
Teachers' Resources
On a sphere of radius $R$ we use a scale factor and the equivalent formula is $$\cos {a\over R} = \cos {b\over R} \cos {c\over R}.$$
All the familiar trigonometric identities in Euclidean Plane
Geometry have their counterparts in Spherical Geometry (otherwise
known as Elliptic Geometry) and also in Hyperbolic Geometry. These
are the geometries on flat surfaces (Euclidean Geometry), on
surfaces of positive curvature (Spherical Geometry) and on surfaces
of negative curvature (Hyperbolic Geometry). See the article
Curvature of Surfaces.
Most of the results in these two other geometries are much more similar in form to the trigonometric identities you meet in school than the result proved here which is equivalent to Pythagoras' Theorem.
The corresponding Pythagorean Theorem for right-angled triangles in Hyperbolic Geometry is: $$\cosh a = \cosh b \cosh c.$$
