Perpendicular Lines
Position the lines so that they are perpendicular to each other. What can you say about the equations of perpendicular lines?
Problem
This problem follows on from Parallel Lines
Alter the positions of the lines by moving the points.
Position the lines so that they are perpendicular to each other.
Try various arrangements.
What can you say about the equations of perpendicular lines?
Getting Started
You may want to take a look at Parallel Lines before attempting this problem.
Take a look at the interactivity below which allows you to move the vertices and make different squares.
The adjacent sides of a square are perpendicular to each other.
How would you describe going from one vertex to the next? And to the next? And to the next?...
Student Solutions
We received correct solutions from Ash and Lucy, two students at Tiffin Girls' School. Well done to you both.
Ash sent us this correct solution:
For example:
Take a random gradient, say $\frac{4}{7}$
The negative reciprocal gradient will be $\frac{-7}{4}$
Make up two equations with these gradients, say
$y =\frac{4x}{7}$ and $y =\frac{-7x}{4}$
Draw them on a grid
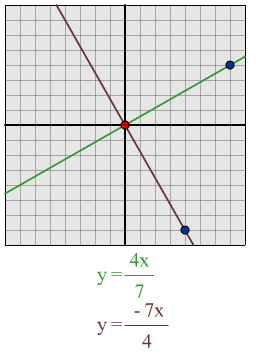
You get perpendicular lines.
Lucy recorded how she worked through this problem:
$y = x$ is perpendicular to $y = -x$
$y = x$ is perpendicular to $y = -x + 2$
$y = 2x$ is perpendicular to $y = -x/2$
$y = -3x$ is perpendicular to $y = x/3 $
$y = -2x$ is perpendicular to $y = x/2 $
I can see a pattern here: when the two gradients of perpendicular lines are multiplied together they give -1, and the y-intercept does not affect if the line is perpendicular or not.
I will now try to work out what the perpendicular line of some other lines will be using this formula:
$y = 7x - 3$:
Using my formula I predict that a line which is perpendicular to this line will be $y = -x/7 - 3$
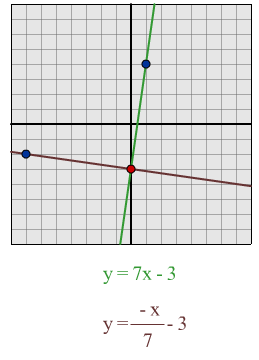
When I tested the lines out, I found that the formula had worked.
$y = x/3 + 4$:
Using my formula I predict that a line which is perpendicular to this line will be $y = -3x + 4$
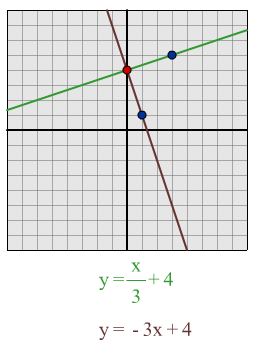
Having drawn out the lines I found that the formula worked and the lines were perpendicular.
$y = -7x/3 + 2$:
I predict that a line which is perpendicular to this line will be $y = 3x/7$
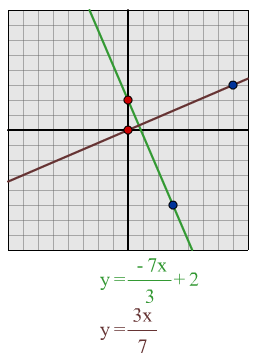
From drawing out these lines I can see that they are perpendicular.
Teachers' Resources
Why do this problem?
This resource allows students to explore the connections between straight lines on graphs and the equations that represent or define them - equations of the form $y = mx + c$.
Possible approach
Take time to discuss how an equation represents a line by defining the set of points that lie along it. If this needs some reinforcement the related problem Parallel Lines might be a good place to start.
Show the interactivity, moving all four points to allow the group to see the freedoms the lines have. Draw attention to the equations of the lines showing beneath the graph.
Ask a student to move the lines so that they are perpendicular. Does everyone agree? How can we be sure? Can anyone set up a harder pair of perpendicular lines? Are they correct? Preliminary work looking at perpendicular lines is suggested in At Right Angles.
Ask students to work in pairs at computers, finding pairs of perpendicular lines and noting their equations. What do they notice about the equations of perpendicular lines? Encourage them to make and test their conjectures. Bring the class together to share insights and conclusions.
When they understand what is going on, ask them to set challenges for each other - either for their partner, or on the board for the whole group:
e.g. find three pairs of perpendicular lines which go through $(2,3)$, find perpendicular lines where one goes through $(-1,3)$ and the other through $(6,2)$...
Key questions
What does perpendicular mean?
How do the equations of perpendicular lines relate to each other and why is that?
Possible support
Concentrate on the work in Parallel Lines
When discussing perpendicularity, ask students to draw tilted squares on the interactivity in Square Coordinates, and/or to do some work drawing them on squared paper. This topic might also provide a good excuse to play the game Square It
Possible extension
Ask students to suggest equations for sets of fourlines that define a rectangle/square/parallelogram, etc. This is described in the problem Enclosing Squares . It would be useful to have graph plotting software available.
