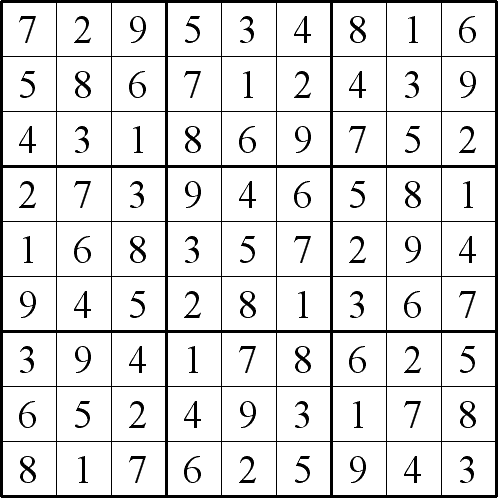
Integrated Product Sudoku
This Sudoku puzzle can be solved with the help of small clue-numbers on the border lines between pairs of neighbouring squares of the grid.
Problem
by Henry Kwok
Image
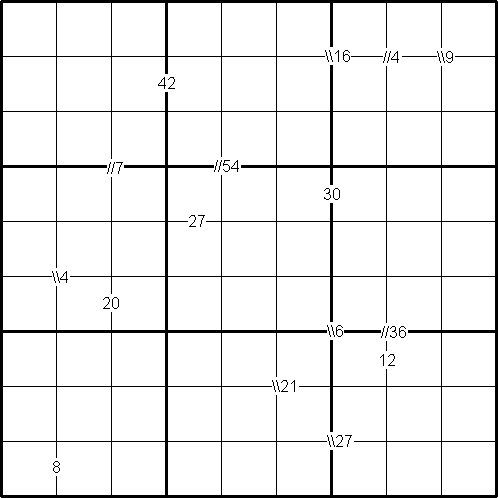
Rules of Integrated Product Sudoku
Like the standard sudoku, this sudoku variant has two basic rules:
- Each column, each row and each box (3$\times$3 subgrid) must have the numbers 1 to 9.
- No column, row or box can have two squares with the same number.
The puzzle can be solved with the help of small clue-numbers which are either placed on the border lines between selected pairs of neighbouring squares of the grid or placed after slash marks on the intersections of border lines between two diagonally adjacent squares.
Each small clue-number is the product of two digits in the two squares that are horizontally or vertically or diagonally adjacent to each other. The position of each pair of diagonally adjacent squares is indicated by either two forward slash marks // or two backward slash marks \\.
For example:
- the //36 on intersection of border lines between the diagonally adjacent squares (6, 8) and (7, 7) means that possible pairs of numbers in the squares are: 4 and 9 or 9 and 4 or 6 and 6.
- the \\6 on intersection of border lines between the diagonally adjacent squares (6, 6) and (7, 7) means that possible pairs of numbers in the squares are: 1 and 6, 6 and 1; 2 and 3, or 3 and 2.
- finally, the clue-number 8 on the border line betweeen the squares (9, 1) and (9, 2) means that possible pairs of numbers for these squares can be from the following combinations: 1 and 8, 8 and 1; 2 and 4, or 4 and 2.
Getting Started
Caitlin kept a record of the order in which she filled the Sudoku.
She filled the cell marked 1 first, then the cell marked 2, then the cell marked 3...
You might like to retrace her route to fill in the cells in the same order, though this is just one possible route through the problem.
You can print her journey here.
Student Solutions
Image