Arrow Arithmetic 1

This problem forms the first part of an investigation into how to represent numbers using geometric transformations that will ultimately lead us to discover numbers that are not on the number line.

I'm going to assume that you are happy with the idea of numbers that lie on the number line. Just to remind you, here is a picture of a small part of the number line.

The plan of action is to develop pictures or geometric representations of the numbers we know about already. We'll also develop ways to add, subtract, multiply and divide using just those pictures. Then we'll change the picture very slightly...

Here's my first attempt at a picture of the number 1. It's simply a blue arrow.

I don't think this is a good enough picture yet, but it's helpful to think about its shortcomings.

Let's try to do arithmetic with these arrows. Try three simple additions.


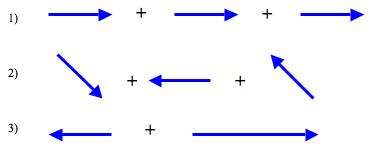
I tried these with three friends and here are the answers they gave me

	Sam	Hannah	Tim
1)	3	3	3
2)	-1	3	3
3)	1	3	2