Rearrange the square
We can cut a small triangle off the corner of a square and then fit
the two pieces together. Can you work out how these shapes are made
from the two pieces?
Problem
Simply cutting a corner off a square can lead to a puzzling activity.
Image

So the little triangle is removed:
Image

This little triangle is then put back making sure that a corner of the triangle is always touching a corner of the shape that the triangle came from, and two edges line up.
We can then make new shapes:
Image

Which were made as follows:
Image

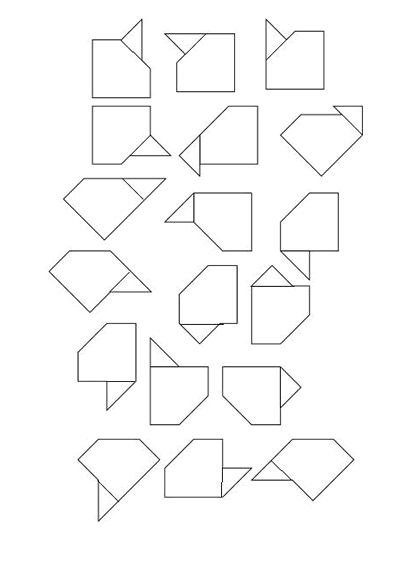
So here's the challenge: Can you make all the following and tell us about how they are made from the two shapes?
Image

Getting Started
You could print off and cut out a square from this sheet.
Can you try to imagine how the two pieces make the shape before trying it out? Were you right?
How about turning the pieces?
You might find it useful to work out first which part of the shape could be the small triangle.
Student Solutions
A pupil from Lauriston School said:
The best way to do this is to do it physically, always look
for the long side.
Louise suggests a different method:
Locate either the short side where the cut was made or three remaining right angles, then draw in the sides of the square, this will allow you to see where the triangle has been placed.
Sam from Godalming College submitted this solution which he says he did by sight:
Image
Well done Sam and thank you everyone for writing in!
Teachers' Resources
This practical investigation will increase children's confidence with manipulating and rotating shapes, and they may even be able to visualise how the pieces fit together before checking.
It would be good to get quite young children having a go at this investigation by providing them with a square piece of card. A pre-drawn line could be useful for some pupils, to help them on their way. The line goes from half way along one edge to half way along an adjacent edge. The triangle can then be cut off and the shape covering explored. Here is a sheet of pre-drawn squares which you may find useful.
Ideally, pupils could work in twos or threes and take turns, having a chat together so that when one solution is suggested it has to be justified to the other(s).
