Twice as Big?
Investigate how the four L-shapes fit together to make an enlarged L-shape. You could explore this idea with other shapes too.
Problem
If we double each side of a small square we get a new enlarged square:
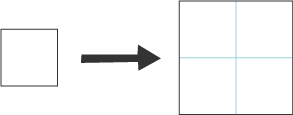
The new enlarged square is the size of four of the smaller squares.
This also happens when we enlarge other shapes. Some, like the squares, can be filled with the same smaller shape.
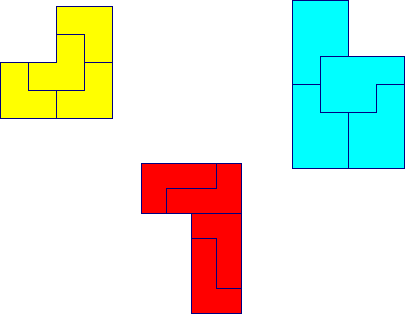
Look at these:
Can you work out how the four shapes fit to make the enlarged shape each time?
You might need to rotate or reflect the smaller shapes to fit them in. (This means that if you make them from squared paper you will need to turn them round or turn them over.) In this interactivity the rotation and the reflection of the shapes has been done for you.
Please send us pictures of your completed shapes.
If you enjoyed working on this problem, you might like to investigate some more shapes. Have a look at Two Squared or print out this sheet which contains some other examples as well as the shapes above.
Getting Started
Try putting one shape in at a time, being careful not to leave any gaps which you won't be able to fill.
If you're not using the interactivity, you might like to use this sheet and cut out the smaller shapes.
Student Solutions
We received several solutions to this problem - thank you to all of you who wrote in, including Ivy, Kelsie and William from Mason Middle School; Issy from Culford Prep and Jessica and Philip from CWBS. Here is the image that Jessica and Philip sent:
We also had suggestions about how to go about tackling the problem, for example by starting at the top and fitting shapes in, then gradually working down. Very good advice!
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
Possible support
Suggest using the interactivity working on one shape at a time from the top.
