A sameness surely
Problem
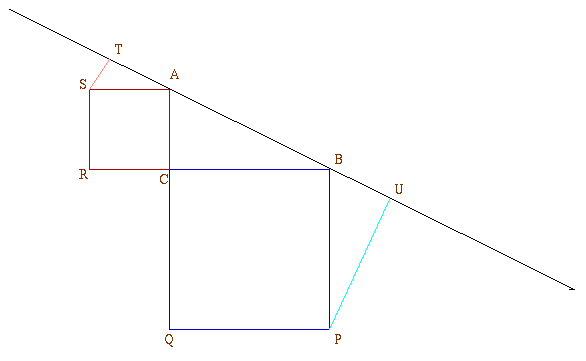
Triangle ABC has a right angle at C. ACRS and CBPQ are squares. ST and PU are perpendicular to AB produced.
Show that ST + PU = AB
Student Solutions
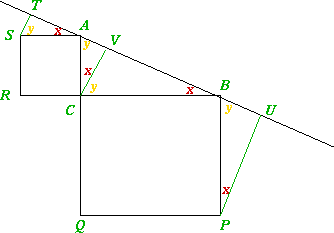
David from Madras College, St. Andrews and Natalie from West Flegg Middle School, Norfolk correctly used congruent (n.b. not similar) triangles to show the sameness, having first constructed an altitude through C parallel to TS and PU. When equal angles and side lengths (SA and AC) are identified it is soon apparent that triangle CVA is congruent to triangle ATS and also that triangle CBV is congruent to BPU. Hence ST + PU = AB.
Jack and Jan at Necton Middle School "discovered that triangle STA together with triangle BUP, when rotated, will fit exactly into triangle ACB........." but don't state about which centres the rotations are to take place.
Another interesting approach here came without a name on it, from West Flegg MS again. This time after drawing CV perpendicular to TU, if you draw two squares one with side TV and the other with side VU , boxing in the original two squares, it is clear to see that ST + PU = AV + VB = AB.
