Resistance
Find the equation from which to calculate the resistance of an
infinite network of resistances.
Problem
Image
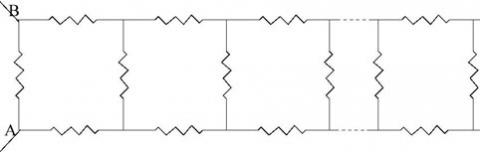
Each resistance in this infinite network is 1 ohm. The 'ladder' extends indefinitely to the right.
Find the total resistance between A and B.
You do not need to know any physics to do this problem. If you read the notes you will see how to write down equations for resistances of networks.
Getting Started
What is infinity plus one? This may be a sufficient hint to help you solve the problem. Have a go before reading any further.
Image
|
One approach to solving problems involving an infinite system
like this one is to focus on the idea of infinity and its
properties. Removing one item from an infinite system does not
change the value for the whole system. This idea is the key to the
simplest method of solving this particular problem.
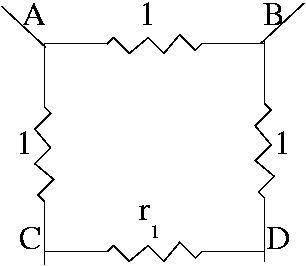
In this diagram the infinite ladder extends downwards and the
network below C and D is effectively the same as the network below
A and B. The total resistance $r_1$ between C and D, for the
infinite network, will be the same as the total resistance $R$
between A and B. So we can think of the resistance between A and B
as a resistance of 1 ohm in parallel with three resistances in
series. Write down the equation and you will get a simple quadratic
equation to solve for $R$.
|
An alternative method is to start with simple cases. When we have an infinite system we often start with $n=1$ and 2, 3, ... and try to find a formula for $n$ and then calculate its limit as ${n\to \infty}$. Very often this method of solving a problem is the best one but not always. In this case the method leads to an infinite continued fraction which can be evaluated to give the required value of the resistance.
Student Solutions
Aleksander from Gdynia Bilingual High School No 3, Poland, David from Guilford County (is that UK, US or elsewhere?) Andrei from Romania and Chris from CSN used different methods to solve this problem, all of them leading to solving a quadratic equation. Chris used the observation that, removing three resistors leaves the resistance of the remaining network unchanged, and quickly arrived at the quadratic equation which gives the solution. Aleksander visualised the network in a different, but equivalent, configuration and used continued fractions and David's method was similar. Andrei arrived at the same quadratic equation by first proving that the sequence of resistances $R_0, R_1, R_2, ...$ from A to B, corresponding to different number of resistance 'squares', is a steadily decreasing sequence and, as $R_n > 0$, the sequence tends to a limit.
This is Chris's solution:
Following the hint, keep in mind that the equations for series resistances and parallel resistances are: $R = R_1 + R_2$ for series and $R = (R_1 \times R_2)/(R_1 + R_2)$ for parallel.
Image

The resistance $R$ between A and B is the equivalent of a
resistance of 1 ohm in parallel with two resistances of 1 ohm and a
resistance R in series and we can write the following equation: $$R
= {1 \times (2 + R)\over 1 + (2 + R)} = {(2 + R)\over (3 + R)}.$$
Reworking the above equation we get: $R(3 + R) = (2 + R)$ or $$R^2
+ 2R - 2 = 0.$$ Solving the quadratic equation we get two
solutions, one of which we cannot use because it is negative, so $R
= - 2.73205$ is not valid because a resistance cannot have a
negative value. The correct solution is: $$R =\sqrt 3 -1 \approx
0.732051.$$
This is Aleksander's
solution:
Generally it is easier to calculate the resistance of a
circuit when you present it in a way that one end of circuit (here
A) is on the left and the other is on the right. Here we have an
illustration of our ladder circuit in such a way making it much
easier to justify whether two resistors are in parallel or in
series.:
Image
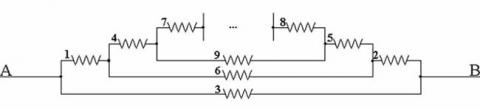
From the picture we know that resistors labeled 1, 2 and the
group of resistors 4,5,6,7,8,9 (all 1 ohm) are connected in series.
We can also observe that the resistor 3 is connected in parallel to
the resistors mentioned before. Therefore, where $R$ is the
resistance of the whole circuit, and $R_n$ is the resistance of the
$n$th resistor, we can write: $$R = {1\over {1\over R_3} + {1\over
R_1 + R_2 +...}}.$$ The three dots refer to the resistances of the
resistors not mentioned in the formula, but occurring in the
further part of the circuit.
We can observe that the pattern for the first three resistors
repeats for the rest so $$R = {1\over {1\over R_3} + {1\over R_1
+R_2 + {1\over {1\over R_6} + {1\over R_4 +R_5+...}}}}$$ and the
fraction grows like that to infinity. As all the resistances are 1
ohm this gives the continued fraction: $$R = {1\over 1 + {1\over 2
+ {1\over 1 + {1\over 2 +...}}}} = {1\over 1 + {1\over 2 + R}}$$
After a few simplifications we obtain the quadratic equation : $R^2
+ 2R - 2 = 0.$ As $R$ must be positive the solution is $R = \sqrt 3
- 1$ ohms.
This is Andrei's
solution:
First I shall prove that the resistance from A to B tends to a
limit as more 'squares' are added to the network. I shall denote
the value of each resistance by $R$ and the values of the
equivalent resistances between A and B, corresponding to different
number of resistance 'squares', by $R_0, R_1, R_2, ... $ etc.
Evidently $R_0 = R$ and $R_1 = 3R/4$.
Image
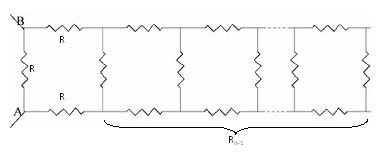
From the diagram I observe that: $${1\over R_n} = {1\over R} + {1\over 2R +R_{n-1}}.$$ where $R = 1$. I observe that $R_1< R_0$, and I shall prove by induction that $R_n< R_{n-1}$. This, by the recurrence relation, is equivalent to: $$R_n< R_{n-1}\Leftrightarrow {1\over R_n}> {1\over R_{n-1}} \Leftrightarrow {1\over R} + {1\over 2R + R_{n-1}} > {1\over R} + {1\over 2R + R_{n-2}}\Leftrightarrow R_{n-1} < R_{n-2}.$$ So, the sequence $(Rn)$ is strictly decreasing. Evidently $R_n > 0$ so the sequence $(R_n)$ is convergent. By considering the limit in the recurrence relation (putting $R=1$), $$\lim _{n\to \infty} R_n = {1\over {1+ {1\over 2 + \lim_{n\to \infty}R_{n-1}}}}$$ where $$\lim _{n\to \infty} R_n = \lim _{n\to \infty} R_{n-1} = R_{L}.$$ This gives $R_{L}= {2+ R_{L}\over 3 + R_{L}}$ and hence the quadratic equation $R_{L}^2 + 2R_{L} - 2= 0$. The positive solution of this equation gives the resistance of the network: $\sqrt 3 - 1$ ohms.
Teachers' Resources
Image
|
When resistances are connected in a line so that the current in the circuit has only one route to take the total resistance is the sum of the separate resistances. The resistances are said to be connected in series . In this diagram the total resistance $R$ is given by $R = R_1 + R_2 + R_3$. |
| When resistances are connected in parallel so that, at a junction, the current flows along more than one route, the reciprocal of the total resistance is the sum of the reciprocals of the separate resistances. In this diagram the total resistance $R$ is given by $${1 \over R} = {1 \over R_1} + {1 \over R_2} + {1 \over R_3}.$$ | Image
|
