All about ratios
A new problem posed by Lyndon Baker who has devised many NRICH
problems over the years.
Problem
Can you work out the distances?
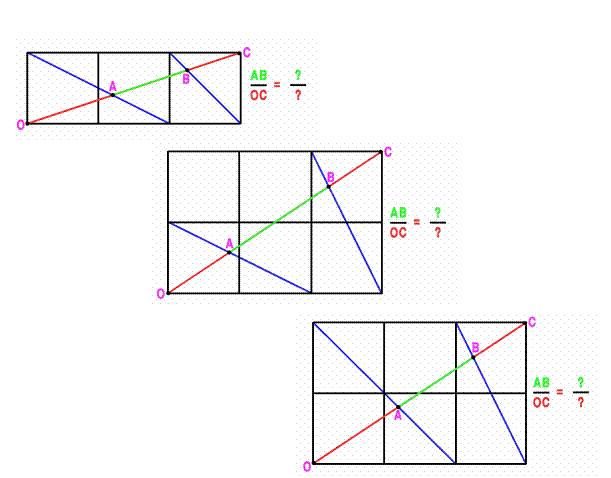
Image
Getting Started
There is a better method using only ratios.
Look for similar triangles.
Look for similar triangles.
Student Solutions
Excellent solutions were sent in by Michael from Wilmslow High School, Cheshire, UK and Andrei from Tudor Vianu National College, Bucharest, Romania.
Image
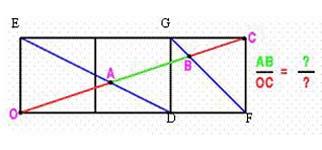
|
(1) As triangles AOD and AEC are similar $${OA\over AC} = {OD\over EC} = {2\over 3} {\Rightarrow}{OA\over OC} = {2\over 5}.$$ As triangles BOF and BCG are similar $${OB\over BC} = {OF\over GC} = {3\over 1} {\Rightarrow} {OB\over OC} = {3\over 4}.$$ Hence: $${AB\over OC} = {OB - OA\over OC} = {3\over 4} - {2\over 5} = {7\over 20}.$$ |
Image
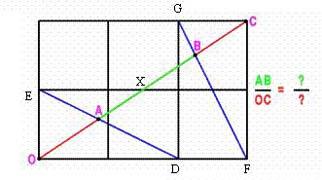
|
(2) From triangles OAD and AXE $${OA\over AX} = {OD\over EX} = {2\over 1.5}= {4\over 3}$$ and hence $${OA\over OX} = {4\over 7} \quad {\rm and} \quad {OA\over OC} = {2\over 7}.$$ Again $${OB\over OC} = {3\over 4}.$$ Hence: $${AB\over OC} = {OB - OA\over OC} = {3\over 4} - {2\over 7} = {13\over 28}.$$ |
Image
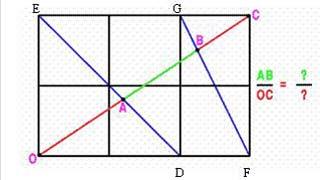
|
(3) The reasoning in this part is identical to part (1). |
Teachers' Resources
Finding several methods can often help us to a better understanding of the mathematics involved, giving us a richer experience than gained from simply finding the answer. Although these ratios can be found using coordinates and finding intersections of lines and distances, this is not the most efficient method.
