Digital Times
Problem
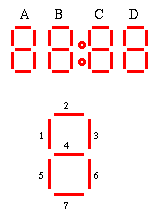
A digital clock shows hours and minutes as illustrated below.
Image

|
| for example 9:38pm is displayed as Image

|
Which segment is lit most each day? Which segment is lit least? Does it make any difference if it is set to 12 hours or 24 hours?
Student Solutions
Hayley of Lytham St Annes High School sent in a beautifully presented word processed solution which we have re-produced here. She did more than the question asked for, calculating how long each segment is lit up in a day rather than simply saying which is lit up for the most time and which for the least time. In the best mathematical style Hayley first set up her notation. Another very good solution was sent in by Helen of Maidstone Girls' Grammar School who used the same notation.
In doing mathematics in real life (as opposed to answering text book or exam questions) the first step is to define the problem precisely and in so doing you must state clearly what is being assumed. This is exactly what Hayley did, she assumed that, until ten o'clock, rather than having no number lit up for digit A, a zero is put there. If you make different assumptions you get different versions of the problem which will, in many cases, have different answers.
- Solution to version 1 of the problem:
- Hayley's solution to version 2 of the problem.
The 12 hour clock
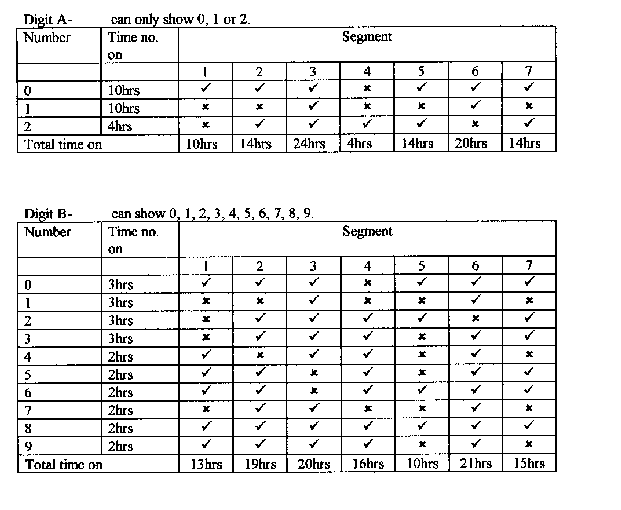
Most Used SegmentSegments 3 and 6 on digit A are on 24 hours a day.
There is either a 0 or a 1 for digit A, and these two segments are
lit for both a 0 and a 1.
It is easy to discount all other digits as they all cycle round every digit, or digits 1-5, and every segment is turned off at some time in this way.
Least Used Segment
Segment 4 on digit A is never turned on, as it is not contained in either the 0 or 1.
You can discount the other segments as they are all turned on at some point.
The 24 Hour Clock
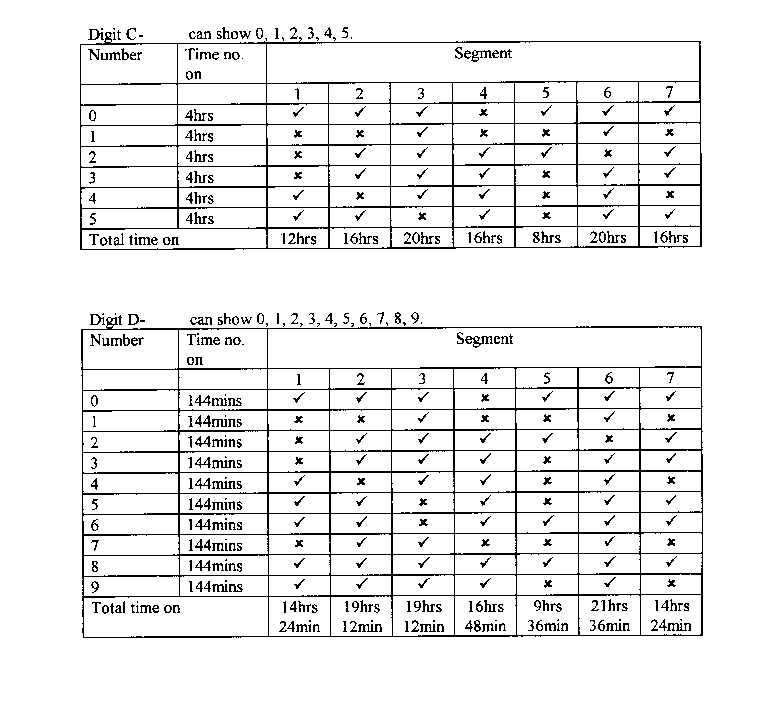
From the following tables you can tell that the segment on for the most time is segment 3 on digit A. As this digit can only have a 0, 1, or 2, this segment is on all the time.
The least used segment on the 24 hour clock is segment 5 on digit C.