Route to Infinity
Can you describe this route to infinity? Where will the arrows take you next?
Problem
Route To Infinity printable sheet
Take some time to look at the route followed by the arrows in this diagram.
Then look away and describe the path to a friend.
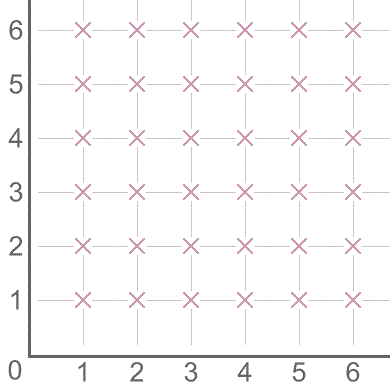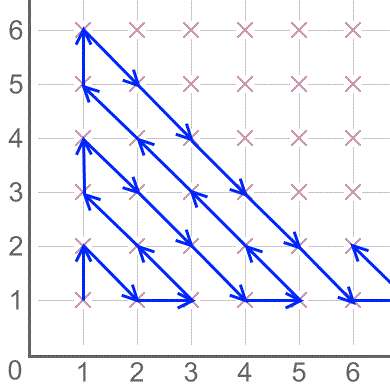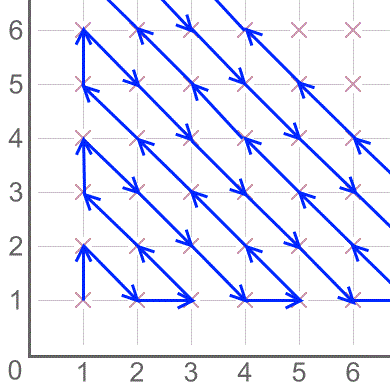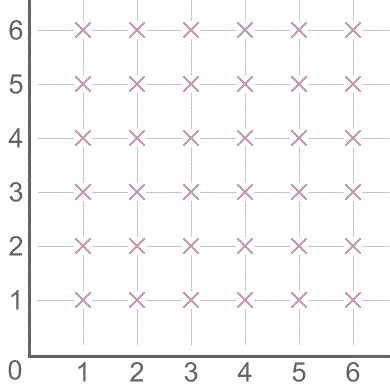
If the pattern of arrows continues for ever, which point will the route visit immediately after (18,17)? Explain how you know.
How many points will be visited before the route reaches the point (9,4)?
Explain how you worked it out.
Which point will be the $1000^{th}$ to be visited?
Getting Started
Take a look at the co-ordinates of the points along the route.
What do you notice about the order in which the route visits the points?
When do the arrows point up, and when do they point down?
Student Solutions
After (18, 17), the route will visit (19, 16). Lots of people got this right - let's have a look at just a few of their solutions:
Tiberiu noticed:
I see that the route goes upwards through the points with coordinates that are equal (eg. 18,18) and downwards through the points with coordinates that are adjacent (eg. 18,17). Therefore the next coordinate is (19,16).
Lawrence, from Chircher's College, worked it out like this:
Looking at the diagram you can tell that if the x coordinate of the bottom right point on a line is even, the arrows in the line go down and right, otherwise, they go up and left. The point (18,17) is on the line with bottom right point (18+17-1,1) = (34,1). Because 34 is even, the arrows go down and right, so the next point is (19,16).
Alex, from Dixons City Academy, spotted the same thing, in a different way:
The numbers all lie on lines with equations x+y=n, where n is some integer. If n is odd, then the line begins at (1, n-1). These arrows point towards the bottom right. If n is even, the line begins at coordinate (n-1, 1) and the direction of the line is towards the top left. Notice that 18+17=35, so the coordinate (18, 17) is on the line x+y=35.
Segev, Adam, Yoav, Daniel and Jonathan from JFS answered the second part of our question:
There are 74 points visited before the route reaches the point (9,4). The number of points visited follows the triangle numbers.
Number of points visited up to (1,1): 1
Number of points visited up to (2,1): 3
Number of points visited up to (1,3): 6
Number of points visited up to (4,1): 10
etc.
Therefore the number of points visited up to (1,11) is 66.
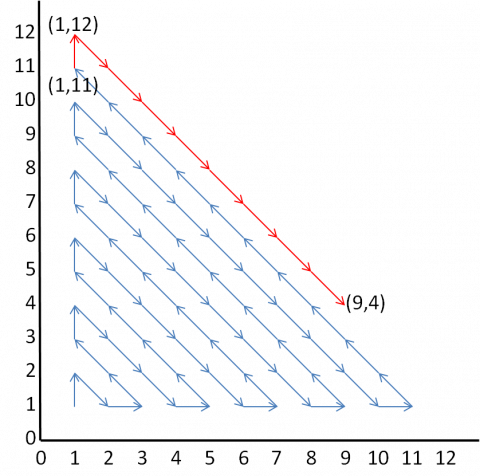
It is worth noticing here that because $9+4=13$ is odd, the line points towards the top left, so we are starting at (1,11).
Then, we need to visit 8 points on the diagonal before reaching (9,4), which are to (1,12), (2,11), (3,10), (4,9), (5,8), (6,7), (7,6) and (8,5) before reaching (9,4).
This is a total of $66+8=74$ points visited before (9,4).
The diagram below shows the 66 steps in blue, and then these final steps in red. Although there are nine red steps marked, only eight are counted as it is the number before (9,4) that is requested.
There were far too many great solutions to list here - thanks to everyone who submitted one!
Teachers' Resources
Why do this problem?
This problem offers a good opportunity for students to discuss images and find convincing arguments for their solutions.
Reuben Hersh has written that:
"In the classroom, convincing is no problem. Students are too easily convinced. Two special cases will do it."
This problem offers an opportunity to ensure that students are justified in generalising from the particular cases that they have selected.
Possible approach
This printable worksheet may be useful: Route To Infinity
You may be interested in our collection Dotty Grids - an Opportunity for Exploration, which offers a variety of starting points that can lead to geometric insights.
Show the diagram. It's available dynamically on a PowerPoint slide, or you could use the poster for a static version of the image.
Possible support
Before working on this problem, spend time on Cops and Robbers and Coordinate Patterns to develop students' fluency with coordinates.
Possible extension
