Who is the Fairest of Them All ?
Explore the effect of combining enlargements.
Problem

You might find it helpful to copy the diagram onto dotty paper.
Enlarge the flag by a scale factor of $2$ about the first centre of enlargement. Now enlarge the resulting flag by a scale factor of $\frac{1}{2}$ about the second centre of enlargement. Can you find a single transformation that takes the first flag to the last flag?
Try this with the flag in different positions, and with different centres of enlargement. Describe what will happen for any two centres of enlargement and a flag in any position.
Now try changing the scale factors so that the first enlargement is by scale factor $3$ and the second by scale factor $\frac{1}{3}$. Try some other similar pairs (remembering that if the first scale factor is $k$ then the second one should be $\frac{1}{k}$).
Describe what will happen if the first scale factor is $k$ and the second $\frac{1}{k}$?
Getting Started
If the flag is enlarged by scale factor $k$ and then by scale factor $\frac{1}{k}$, how large will it be at the end? Will it have changed the way it is facing?
You might find it useful to use vectors for the proof at the end of this question. For example, you could write $\mathbf{x}$ for the vector from the first centre of enlargement to the second centre of enlargement, and $\mathbf{a}$ for the vector from the first centre of enlargement to the foot of the flagpole. If you can prove your answer for the foot of the flagpole, do you need to do any extra work to prove it for the rest of the flag?
Student Solutions
Isabel from St Andrew's Scots School in Argentina used Geogebra to investigate the problem. This is Isabel's work, with some teacher comments.
Robert from Kings Ely said this very concisely:
The vector for the flags is $\frac{n-1}{n}$ of the vector of centres.
See if you can follow this explanation of why this is the result using this diagram:
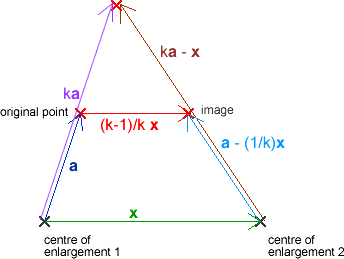
Suppose the first scale factor is $k$ (so the second one is $\frac{1}{k}$). Let $\mathbf{x}$ denote the vector from the first centre of enlargement to the second. Then the required transformation is a translation by the vector $\frac{k-1}{k}\mathbf{x}$.
To see this, consider a single point on the flag. (If we show that the required transformation for a single point is the given translation, then the same will apply to the flag.) Let $\mathbf{a}$ denote the vector from the first centre of enlargement to the point. Then the vector from the first centre of enlargement to the image of the point under the first enlargement will be $k\mathbf{a}$. The vector from the second centre of enlargement to this image will be $k\mathbf{a}- \mathbf{x}$, so the vector from the second centre of enlargement to the final image will be $\frac{1}{k}\left(k\mathbf{a}-\mathbf{x}\right) =\mathbf{a}-\frac{1}{k}\mathbf{x}$. So the vector from the initial point to the final image will be $-\mathbf{a}+\mathbf{x}+\mathbf{a}- \frac{1}{k}\mathbf{x}=\frac{k-1}{k}\mathbf{x}$, as required.
Teachers' Resources
Why do this problem?
This problem is the third of three related problems. The first problem is Mirror, Mirror... , and the second is ...on the Wall . All three problems ask students to consider the effect of combining two transformations, and then challenge them to describe the single transformations that produce the same results.
This problem follows on from the other two but works equally well on its own. It could be used as extension work for students learning to draw enlargements from a centre of enlargement, using fractional scale factors.
Alternatively, this problem/series of problems could provide suitable task(s) for a unit of work on combined transformations. Some knowledge of vector algebra might be useful for students attempting a full proof.
Possible approach
This printable resource may be useful: Who is the Fairest of Them All?.
As an extension task, all that is needed is to provide the problem as a worksheet to pairs of students who could then make sense of it together. When they have established the combined transformation for one specific example, a teacher intervention may be appropriate, to move the focus to the general case, asking the key questions below.
Key questions
What if the flag was in a different place?
Possible support
Spend time drawing accurate enlargements. In theclass/group every enlargement could be drawn on paper with full details written on and signed; then every student could alternate between doing an enlargement and checking one off the pile.
Possible extension
Ask students to summarise their findings in exactly 20 words (!) then ask if there is anything further that might be varied.
