...on the Wall
Explore the effect of reflecting in two intersecting mirror lines.
Problem
...on the Wall printable sheet
This problem follows on from Mirror, Mirror...
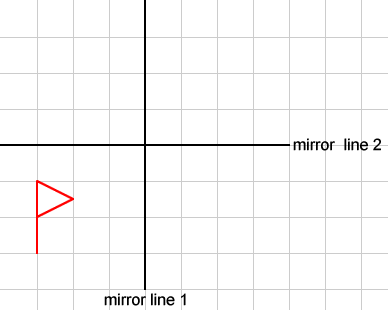
You might find it helpful to copy this diagram onto squared paper.
Reflect the flag in one of the lines.
Reflect the resulting image in the other line.
Can you describe the single transformation that takes the first flag to the last flag?
Does it matter in which line you reflect first?
Try this with the flag in other positions.
In each case, what is the single transformation that takes the first flag to the last flag?
Now try it with lines that meet at $45^{\circ}$ and at $60^{\circ}$ (you might find it helpful to use isometric paper for the $60^{\circ}$ case).
Again, try it with the flag in different positions
Can you describe the single transformation that takes the first flag to the last flag when the lines meet at $\theta^{\circ}$ (theta degrees)?
Getting Started
Student Solutions
Isabel from St Andrew's Scots School in Argentina used Geogebra to investigate the problem. This is Isabel's work, with some teacher comments.

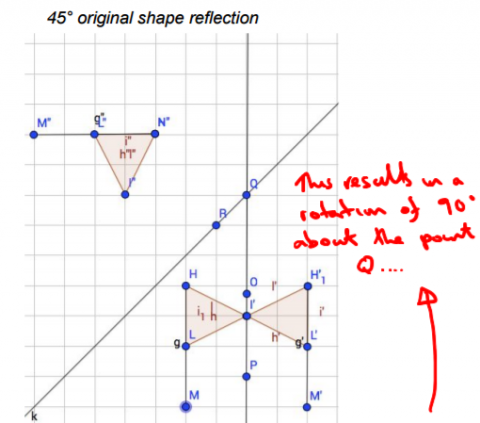
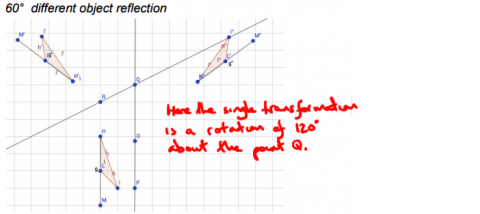
Wenchi, also from St Andrew's Scots School, noticed a pattern for mirror lines that are not perpendicular:
There is a pattern when the mirror lines cross different angles. Reflecting in 2 is equal to 1 rotation by $2\theta$ about the point of intersection of the lines, where $\theta$ is the angle between the lines.
When the lines cross at $45^\text o$, the object rotates by $90^\text o$, and when the lines cross at $60^\text o$, the object rotates $120^\text o$.
Notice that applying this rule to lines which cross at $90^\text o$ gives a rotation of $180^\text o$, as we have already seen.
Here is our explanation of the transformations required in the general case of mirror lines at any angle :
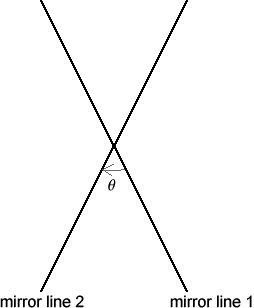
The resulting transformation is a rotation by $2\theta$ about the point of intersection of the lines. If the direction of the angle $\theta$ is from the first line of reflection to the second, then the direction of rotation is the same as the direction of $\theta$.
You should probably check that the same thing works if you reflect in the further line first (remembering that this means the direction is reversed), and if the flag is between the two lines.
We just need to check the result for a single point, because then every point will rotate by the same amount and so the flag will remain intact (and will have rotated by the same amount).
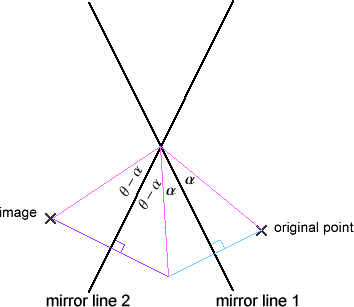
The diagram says it all, really: the line segment joining the point to the origin has rotated by an angle of $\alpha+\alpha+(\theta-\alpha)+(\theta -\alpha)=2\theta$ in the direction of $\theta$.
Teachers' Resources
Why do this problem?
This problem follows on from Mirror, Mirror... but it works equally well on its own. It could be used as extension work for students learning to draw reflections accurately.
Alternatively, this problem and the two related problems Mirror, Mirror... and Who Is the Fairest of Them All? could form a unit of work on combined transformations. All three problems ask students to consider the effect of combining two transformations, and then challenge them to describe the single transformations that produce the same results.
Possible approach
These printable resources may be useful: ...on the Wall, squared paper, isometric paper.
As an extension task, all that is needed is to provide the problem verbally or as a worksheet to pairs of students who could then make sense of it together. When they have established the combined transformation for one specific example, a teacher intervention may be appropriate, to move the focus to the general case -asking the key questions below.
Key questions
What if the flag was in a different place?
Possible support
Ensure students use square paper and encourage them to draw their reflections accurately.
Possible extension
Ask students to summarise their findings in exactly 20 words (!) - then ask what other transformations might be combined in a similar manner.
