 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
...on the Wall



...on the Wall printable sheet
This problem follows on from Mirror, Mirror...
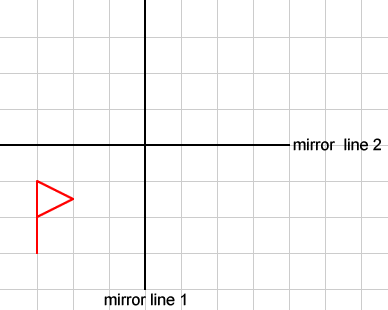
You might find it helpful to copy this diagram onto squared paper .
Reflect the flag in one of the lines.
Reflect the resulting image in the other line.
Can you describe the single transformation that takes the first flag to the last flag?
Does it matter in which line you reflect first?
Try this with the flag in other positions.
In each case, what is the single transformation that takes the first flag to the last flag?
Now try it with lines that meet at $45^{\circ}$ and at $60^{\circ}$ (you might find it helpful to use isometric paper for the $60^{\circ}$ case).
Again, try it with the flag in different positions
Can you describe the single transformation that takes the first flag to the last flag when the lines meet at $\theta^{\circ}$ (theta degrees)?