Mirror, Mirror...
Explore the effect of reflecting in two parallel mirror lines.
Problem
Mirror, Mirror... printable sheet
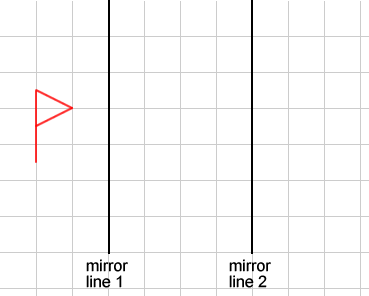
You might like to copy the diagram above onto squared paper to help you with this problem.
Reflect the flag in the left-hand line, and then reflect the image you obtain in the right-hand line.
Can you describe the single transformation that takes the first flag to the last flag?
Repeat this with flags in different positions and orientations, and with different pairs of parallel lines.
Does it matter in which line you reflect first?
Does it matter whether the flag is to one side of the lines or between the lines?
Can you describe the single transformation that takes the first flag to the last flag for any pair of parallel lines?
If you have enjoyed this problem, why not have a go at ...on the Wall and Who is the fairest of them all? ?
Getting Started
If the flag is reflected twice, which way will it be facing at the end?
Thinking about the distance between the lines of reflection might help --- squared paper might be helpful for this.
Student Solutions
Isabel from St Andrew's Scots School in Argentina used Geogebra to investigate the problem. This is Isabel's work, with some teacher comments.
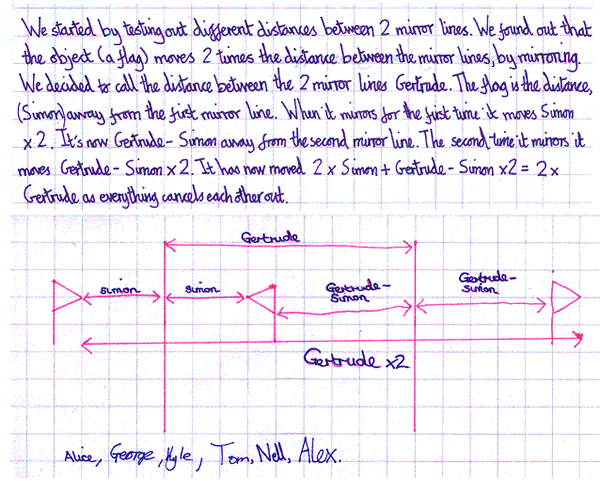
Alice, George, Kyle, Tom, Nell and Alex from Gorseland Primary School explained why this happens:
Isabel went on to investigate what happens for different shapes, and if the shape is reflected in the other mirror line first.
Teachers' Resources
Why do this problem?
This problem could be used as an extension task once students have learnt to draw reflections accurately. It can provide a valuable mathematical challenge for students who are ready to move on while others in the class need more practice with their basic drawing skills.
Alternatively, this problem and the two related problems ...on the Wall , and Who Is the Fairest of Them All? could form a unit of work on combined transformations. All three problems ask students to consider the effect of combining two transformations, and then challenge them to describe the single transformations that produce the same results.
Possible approach
This printable resource may be useful: Mirror, Mirror...,
As an extension task, all that is needed is to provide the problem as a worksheet to a pair of students who make sense of it together. When they have established the combined transformation for one specific example, a teacher intervention may be appropriate, to move the focus to the general case - asking the key questions below.
With a full class, encourage different students to start with slightly different spacings of parallel lines and flag positions. The teacher intervention above could become a full class discussion. Students could regroup according to similarities/differences in the final combined transformations in order to acquire more information without needing to do a lot more drawing.
Key questions
What if the flag was in a different place?
Possible support
Do some introductory reflection work - filling in missing halves of shapes, reflecting patterns in vertical, horizontal and diagonal lines, etc.
Ensure students use squared paper and encourage them to draw their reflections accurately.
Possible extension
Ask students to summarise their findings in exactly 20 words (!) - then ask what would happen if the lines were not parallel (ie. Move them on to ...on the Wall)
