Corresponding Sudokus
This is the second article that looks at aspects of Sudoku. You might find it useful to read the first article before continuing here.
In this article I am going to look af Sudoku puzzles (which I call "Corresponding Sudokus").
These Sudoku puzzles come in matching groups with each of the nine digits in one of the member puzzles having a consistently matching (or corresponding) value in another. So, for example, anywhere a 6 appears in one puzzle a 4 appears in a matching puzzle.
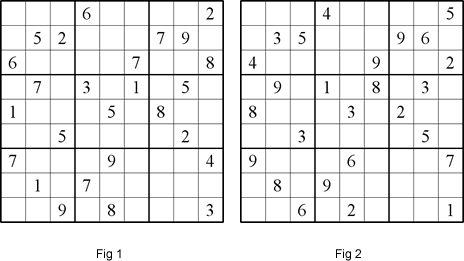
At first glance, the above two Sudoku puzzles (Fig 1 and Fig 2) look different to each other. On closer scrutiny, however, we can see that they are related to each other in some ways.
- Firstly, they have the same number of starting digits,
- Secondly, each starting digit in one puzzle corresponds in position to its counterpart in the other puzzle.
- Thirdly, the starting digits 1 to 9 in the first puzzle correspond to 8, 5, 1, 7, 3, 4, 9, 2 and 6 respectively in the second puzzle.
Now let's look at the puzzle in Fig 3. It has small clue-numbers placed on its border lines. Each clue-number is the difference between the two numbers that should be in the adjacent cells just to the left and to the right from that clue-number. The object of the puzzle is similar to a standard Sudoku, to fill in the whole 9x9 grid with numbers 1 through 9 (one number per cell) so that each horizontal line, each vertical line, and each of the nine 3x3 squares (outlined with the bold lines) must contain all the nine different numbers 1 through 9.
As a solver, you will be groping in the dark for the solution to this Sudoku and the reason for this lies largely in the fact that this variant has two sets of solutions. Hence I call it "Blindfold Sudoku". Not only are there two solutions but they are corresponding Sudokus.
To change the puzzle to one with only one solution, we can insert a starting digit in any cell (e.g. digit 9 in the last column of Fig 3 row 6). The single starting digit acts like the Pole Star to guide the solver out of the "wilderness" of the puzzle and therefore "fixing" the solution. Hence the Sudoku variant created by doing this is called a "Pole Star Sudoku" and is published elsewhere on the site for you to solve.
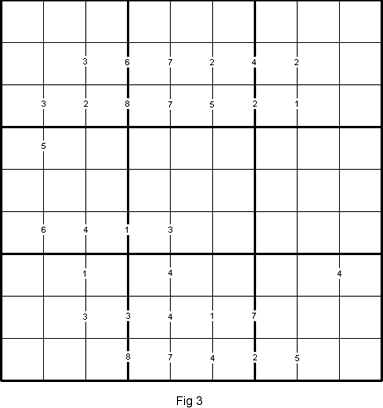
Another way to change the "Blindfold Sudoku" to a variant with a single solution is to add the symbols > and < to every clue-number 1 on the border lines. In other words, change it to a "Duplex Difference Sudoku" as shown in Fig 4.