Spiroflowers
Analyse these repeating patterns. Decide on the conditions for a
periodic pattern to occur and when the pattern extends to infinity.
Problem
A spirolateral is a continuous path drawn by repeating a sequence of line segments of lengths $a_1, a_2, a_3, ... a_n$ with a given angle of turn between each line segment and the next one. (Alternatively the path can be considered as a repeated sequence of 'bound' vectors: $\overrightarrow {P_1P}_2, \overrightarrow{P_2P}_3,... \overrightarrow{P_n P}_{n+1}$, each vector starting at the endpoint of the previous vector.)
Image
|
Image
|
Image
|
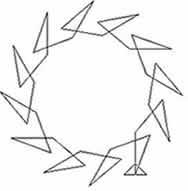
In the first diagram the lengths of the line segments are
equal and the angles of turn vary periodically in sequences of
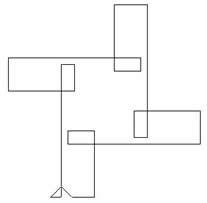
length 3. In the second diagram the lengths of the line segments
vary periodically in sequences of length 5 and the angles of turn
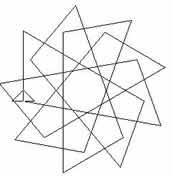
are equal. In the third diagram both the lengths and the angles
vary.
Investigate these patterns, give sequences of instructions
which would produce similar paths and explain why in each case the
spirolateral paths are closed producing a cyclic pattern when the
sequence is repeated infinitely often.
Image
|
Why does the spirolateral in this diagram continue indefinitely, shooting off to infinity if the sequence is repeated infinitely often? |
Getting Started
In all three cases find the number of cycles that are repeated to give the complete path and deduce the total turn for each cycle.
Use Logo to give the instructions for drawing the pattern. Design some patterns of your own.
You do not need to have met the Logo programming language previously in order to do this question. You can download the free MSWlogo program from http://www.softronix.com/logo.html
If you have not used Logo before then, from the first part of this simple introduction to Logo for beginners, you can learn enough in five minutes to use Logo to experiment in drawing the spirolaterals.
Student Solutions
This solution was sent in by Chris who is about to start at Oxford University.
My instructions will all be in the form draw $([a_1,a_2...,a_n],[\theta_1,\theta_2,...,\theta_n])$ and my angles will be in degrees.
There are three types of graph; one that is periodic, one that shoots off and grows without bound, and one that stays within a certain space but is not periodic.
Those of the third type are the easiest to define mathematically. For example draw $([20],[19\pi])$ which appears to start drawing a pentagon but does not quite connect up, instead continuing to loop round taking a slightly different path each time.
Graphs which stay in a closed space but are not periodic occur simply when $S_{\theta} = \theta_1+\theta_2+....+\theta _n$ is not rational . This is because, after turning through each angle once, the pen has turned through $S_{\theta}$ degrees. If $S_{\theta}$ is not rational then no matter how many times the instructions are carried out, the pen will NEVER face the same way twice so cannot be periodic and cannot continue in a straight line overall.
So how can we be sure they only exist within a finite area? If we again consider the position of the pen after it has executed some instructions such that it is on the starting point $a_0,\theta_0$ again then it has moved distance $a_x$, which is zero 'vectorally', and turned through angle $S_\theta$ which is irrational. Now draw $([a_x],[S_\theta])$ which will always curl round on itself and would obviously be restrained to a finite area so therefore the whole graph must also be within a finite area.
The second set of graphs that shoot off and grow without bounds are created when some instructions have been carried out such that $([a_1],[\theta_1])$ are the next instructions, and the pen is some distance greater than zero away from the starting position and facing the same way as when it started. The pen has now travelled distance $a_x \neq 0$ and since it is facing the same direction will carry on in a straight line as long as the instructions are followed, i.e. the instructions will follow two rules:
1) $k\times S_\theta/T_\theta = 0 {\rm mod}\ 360$
where $S_\theta$ is the sum of all the angles, $T_\theta$ is the total number of angles and $k$ is the lowest common multiple of the (number of length instructions) and the (number of angle instructions).
2) After $k$ steps, the total distance moved is greater than zero.
To calculate this, call $\theta_n$ the angle the pen is facing after $n$ steps. If $a_1\cos \theta_1+a_2\cos \theta_2 +...a_k\cos \theta_k \neq 0$ or $a_l\sin\theta_1+a_2\sin\theta_2+...a_k\sin\theta_k \neq 0$ then, after $ k$ steps, the total distance moved is greater than 0.
The set of periodic graphs issubject to two rules:
1) $S_\theta$ is rational.
2) If $k\times S_\theta = 0 \ {\rm mod}\ 360$ then the total distance moved after $k$ steps is 0.
|
In the first diagram the total turn for each cycle is 330 and
as $12\times 330 = 11\times 360$ the path returns to the starting
point after 12 repetitions of the cycle and a total turn of 11
complete revolutions. The program in Logo is:
repeat 12 [fd 50 rt 40 fd 50 rt 130 fd 50 rt 160]
(where fd 50 means go forward a length 50 units and rt 40
means turn right, i.e. clockwise, through an angle of 40 degrees)
|
Image

|
Image
|
Adding the three vectors which make up a cycle (e.g $\vec
{AB}+\vec {BC} +\vec {CD}$) is a simple exercise intrigonometry.
The problem reduces to the same problem as in the
Spirostars case because, joining the starting points of
successive cycles gives line segments of constant length with a
constant angle of turn of 30 degrees between each line
segment.
|
Image

|
In this diagram the total turn for each cycle is 450 degrees.
As $4\times 450 = 5\times 360$ the path returns to the starting
point after 4 repetitions of the cycle and a total turn of 5
revolutions. The program is:
repeat 4 [fd 100 rt 90 fd 10 rt 90 fd 20 rt 90 fd 50 rt 90 fd
25 rt 90 ]
In this case by joining the starting points of successive
cycles we get line segments of constant length with a constant
angle of turn of 90 degrees between each line segment.
|
|
In this diagram the turn for each cycle is 200 degrees. As
$9\times 200 = 5 \times 360$ the path returns to the starting point
after 9 repetitions of the cycle and a total turn of 5 revolutions.
The program is:
repeat 9 [fd 100 rt 120 fd 200 rt 80]
In this case, by joining the starting points of successive
cycles we get line segments of constant length with a constant
angle of turn of 40 degrees between each line segment.
|
Image

|
Image
|
In the case where the graph continues off to infinity the vectors joining the starting points of successive cycles are all in the same direction so the patterns repeat themselves over and over again along a parallel strip. |
Teachers' Resources
The spiropath contains a pattern which is repeated over and over again with different starting points and in different initial directions. Imagine replacing each pattern by a single line segment joining the starting point and end point of that pattern (or equivalently by the single vector which is the sum of all the vectors forming a single example of the pattern). Then the repeated pattern reduces to repeated vectors of the same length end to end with a given angle of turn between the vectors, so the question of whether the path will close up reduces to considering the result of the Spirostars problem .
The diagrams given contain a small triangle which is the Logo 'turtle'. As the path is drawn by the Logo software you can see the turtle moving around. It can be hidden but we have chosen to show it to indicate astarting point and initial direction for the spiropath.
If we define a 'turtle' as a point and a direction, we can use the notation $(x, y, \theta)$ or $(z, \theta)$ or $ze^{i\theta}$. The motif which forms the pattern in the spiropath is repeated but from a different starting point each time and, in general, with a different initial direction. Each repetition of the set of instructions which draws the motif has the effect of mapping turtles to turtles where the turtle gives the initial point and the initial direction. These motifs have the same form but different starting points and initial directions. When the motif is repeated over and over again it may return to the same initial 'turtle' and repeat a cyclic pattern as in the first three examples, or it may never return to a previous starting point and path may go on to infinity.
