Spirostars
A spiropath is a sequence of connected line segments end to end
taking different directions. The same spiropath is iterated. When
does it cycle and when does it go on indefinitely?
Problem
Image
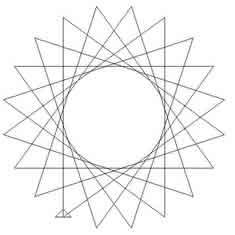
|
To produce this star, twenty line segments of equal length are
drawn in a continuous path, with equal angles between consecutive
line segments.
Imagine instructing a small creature to walk along the path.
You would give the instruction to walk forward a certain distance
then to turn through a certain angle and to repeat the instruction
over and over again.
To do this, you could use the Logo commands:
repeat 20 [forward 100 right $\theta$]
|
Experiment with the Logo program
repeat $q$ [forward 100 right $\theta$]
What shapes can you draw? Vary $q$ and $\theta$. For what values of $\theta$ can you find closed paths (returning to the starting point)?
Prove that the path is closed if and only if $\theta$ is a rational multiple of 360 degrees.
Compare this property to the results found in the problem Stars.
Getting Started
First prove that the line segments are chords of a circle. Then prove that the angle of turn between one chord and the next is equal to the angle subtended by the chord at the centre of the circle.
You do not need to have met the Logo programming language previously in order to do this question. You can download the free MSWlogo program from http://www.softronix.com/logo.html
If you have not used Logo before then, from the first part of this simple introduction to Logo for beginners , you can learn enough in five minutes to use Logo to experiment in drawing the spirostars.
Try repeat 1000 [fd 200 rt 360*sqrt 2]
What happens?
Student Solutions
Chris, who did not reveal his school, sent the following:
Working in degrees, if $\theta$ divides 360 then the shape will be a regular polygon. Else if $\theta$ is rational, the shape will be a star. If $\theta$ is irrational then a 'donut' shape will eventually be drawn, i.e. a star with infinitely many points.
Consider theta being irrational. No matter how many turns are made, the pen will never be pointing in the same direction so cannot repeat its path.
To complete the solution to this problem, consider the diagram:
Image
|
First think: 'why do the points lie on a circle?' We should
not take for granted that they do so we must first prove it.
Draw the perpendicular bisectors of the line segments $AB$ and
$BC$, then the intersection of the perpendicular bisectors is
equidistant from $A$, $B$ and $C$ and thus it is the centre of the
circle with $AB$ and $BC$ as chords. All the perpendicular
bisectors of the line segments in the path will meet in a single
point $O$ equidistant from the endpoints of the line segments.
Therefore all the line segments are chords of a single circle with
centre $O$.
The angle of turn between the equal chords $AB$ and $BC$ in
the path is $\angle PBC = \theta$. Triangles $AOB$ and $BOC$ are
isosceles and $\angle OAB = \angle OBA = \angle OBC = \alpha$. Then
(using angles on a straight line and angles in a triangle) $\theta
= 180 - 2\alpha = \angle AOB$.
|
Consider radii drawn from the centre to the ends of $n$
consecutive chords in the path....
Now can you prove that the path is closed if and only if
$\theta$ is a rational multiple of 360 degrees? Consider radii
drawn from the centre to the ends of $n$ consecutive chords in the
path. The sum of angles between the radii is equal to the total
angle turn $n\theta$ so the path is closed if and only if the total
angle turn is an integer multiple of 360 degrees, that is if and
only if $n\theta = 360m$ or, equivalently $\theta$ is a rational
multiple of 360 degrees.
So consider $\theta = 360 {p\over q}$ where $p$ and $q$ are
positive integers and $p< q$. If the angle of turn is more than
360 degrees, complete revolutions can be discounted, so effectively
$\theta = 360 {p*\over q }$ produces the same path as $\theta = 360
{p\over q}$ where $p* \equiv p$ mod $q$.
If $p$ is a factor of q, (say $q = kp$) then the path is a
regular $k$ sided polygon because the total angle turned when $k$
chords are drawn is $k \times {360\over k}= 360$ degrees.
If $p$ and $q$ are not coprime then $sp=tq$ for some integers
$s$ and $t$ so that the total angle turn with s chords is $s \times
360{p\over q} = 360t$ which is an integer multiple of 360 degrees
so the path is a star with $s$ points. If $p$ and $q$ are coprime
then the path is a $q$ pointed star.
Teachers' Resources
This challenge extends other NRICH challenges which present the same mathematical system for exploration in different ways by different groups of learners: 'Round and round the circle', Path to the stars' and Stars. In the first and last of these you will find interactivities for experimenting with these ideas. In Stars there are downloadable pdfs so you can print out circles with different numbers of equally spaced dots around the circles for paper and pencil explorations.
Celia Hoyles once said that the best mathematical problems challenge people of all ages by providing some questions that everyone can answer, and aesthetically pleasing patterns that everyone can appreciate, while at the same time leading to more challenging questions and more general conjectures which require sophisticated arguments and rigorous proofs.
Image
|
Lynne McClure introduced us to the activity where, given
enough space and enough string, a whole class can stand in a circle
and the string can be passed from one person to another to form a
star.
Suppose there are $q$ people in the circle and the string is
passed to the $p$th person around the circle each time. This leads
to many questions about symmetry, about how the stars are formed,
about why the activity sometimes produces regular polygons, and
about how many different stars can be formed for a given $q$ by
varying $p$.
|
Variants of this activity are provided by using a circular
geoboard, or in
this interactivity which is a virtual geoboard, or by drawing
on a printed sheet with dots around the circumferences of
circles
All these activities presuppose that the points lie on a
circle and the angle of turn is a rational multiple of 360 degrees
and in this problem we make neither assumption.
This problem leads on to more general questions about
spirolaterals. In the question
Spiroflowers we consider what happens if the lengths of the
line segments in the path are varied and what happens if both the
lengths of the line segments and the angles of turn are
varied.
