Hypotenuse Lattice Points
Problem
|
The triangle OMN has vertices on the axes with whole number
co-ordinates.
Points which have whole number coordinates are called lattice
points.
How many lattice points are there on the hypotenuse MN?
|
Image
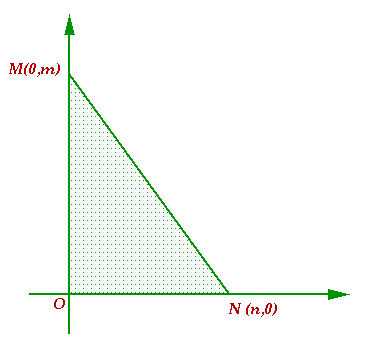
|
Getting Started
Student Solutions
The triangle OMN has vertices M(0,m) and N(n,0) with whole number co-ordinates and we have to find how many lattice points there are on the hypotenuse MN.
The hint here was "First test what happens when m and n are
co-prime (have no common factor)", so this tells you that somehow
the problem involves common factors.
Absolutely the best way to learn is to make mistakes (generally if
you make none then the maths has not got enough challenge in it for
you).
A solution was sent in with a graph drawn for m=27 and n=20, and
the line looked as if it went through the point (3, 23) but it
actually goes through (3, 22.95). You have to check things like
this. One way is to draw the line yourself, decide what you think
about it, then check using a graphic calculator and using the trace
function which will give you readings of the co-ordinates of the
points on the line. ... When you go 20 squares in the x-direction
you have to go DOWN 27 squares in the y direction. You can't divide
this big step into smaller steps going across and down by whole
number changes. [If you use other numbers which have a common
factor, instead of 20 and 27, then there will be smaller steps
between points on the line which have whole number
co-ordinates].
Think about the line extended on and on in the example above. It
has equation:
27 x + 20 y = 540
and we are looking for whole number solutions to this equation (a
Diophantine equation).
We know that x = 0, y = 27 is a solution and if there is another
solution with a bigger x then it will go with a smaller y .
Looking at this equation we see that 20 divides exactly into 540 -
20y so x has to be a multiple of 20. Similarly y has to be a
multiple of 27. Solutions are given by points on the line with
integer co-ordinates and they are:
. . , (-20, 54), (0,27), (20, 0), (40, -27), . . .
When you go 20 squares in the x -direction you have to go DOWN 27
squares in the y direction. There are no solutions in the first
quadrant apart from the points on the axes.
The following is a short general proof of this result:
Theorem
If m and n are co-prime then there are no lattice points on the
line between M(0, m) and N(n, 0) in the first quadrant.
Proof
The line MN has equation mx + ny = mn
Suppose (p,q) is the lattice point on MN and we have
mp + nq = mn (1)
We see from (1) that n must divide nq so that, if m,n are co-prime,
then m must divide q so q = 0 or q = m
Similarly n divides mp so p = 0 or p = n. The only two lattice
points are the points M and N.
In the example given with m = 27 and n = 20. The only 2 lattice
points are the points M and N.
In the example given with m = 27 and n = 20 the general points with
whole number co-ordinates are given by:
x = 20t, y = 27 - 27t (where t is any integer).
Now you will need to do some work to check that when the greatest
common divisor of m and n is the number 2, so that m = 2r and n =
2s where r and s are co-prime, this introduces one lattice point
between M and N.
Next, if the greatest common divisor is 3, there will be two lattice points between M and N, and so on.
We use the notation gcd(m,n) for the greatest common divisor of m and n, so for example gcd(30, 70) = 10.
The general answer is that the number of lattice points (including M and N on the axes) is 1 + gcd(m,n).
