Oranges and lemons, say the bells of St Clement's
Bellringers have a special way to write down the patterns they ring. Learn about these patterns and draw some of your own.
Problem
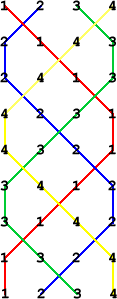
Getting Started
The first three rows for six bells will be:
Student Solutions
We received correct solutions from Alex, Alice, George, Nell and Tom from Gorseland School, Oliver, Edward, Alex and Paul from Dartford Grammar School, Katie from Bathurst West PS, Adam, Annie, Vijay, Louise, Jude, Aaron and Mary from St. Mary Star of The Sea, Ben from Victoria College, Bethany, Alicia and Grace from Willaston Primary School, Samantha and Frances from St. Alban's Catholic Primary School and Max and William from Brenchley and Matfield School. Well done to you all.
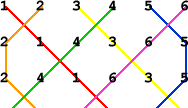
Alex, Alice, George, Nell and Tom sent in this diagram showing the paths of the six bells:
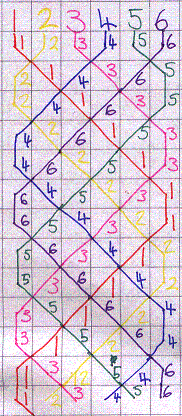
The pattern of the paths for eight bells was sent by Edward:
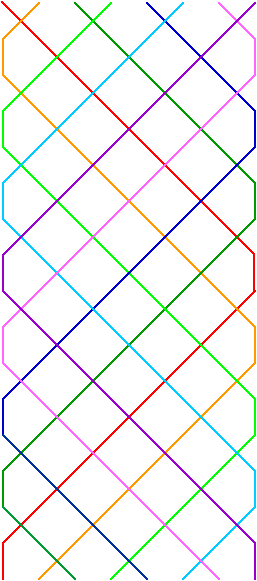
Max and William also sent us a solution for twelve bells!
2 1 4 3 6 5 8 7 10 9 12 11
2 4 1 6 3 8 5 10 7 12 9 11
4 2 6 1 8 3 10 5 12 7 11 9
4 6 2 8 1 10 3 12 5 11 7 9
6 4 8 2 10 1 12 3 11 5 9 7
6 8 4 10 2 12 1 11 3 9 5 7
8 6 10 4 12 2 11 1 9 3 7 5
8 10 6 12 4 11 2 9 1 7 3 5
10 8 12 6 11 4 9 2 7 1 5 3
10 12 8 11 6 9 4 7 2 5 1 3
12 10 11 8 9 6 7 4 5 2 3 1
12 11 10 9 8 7 6 5 4 3 2 1
11 12 9 10 7 8 5 6 3 4 1 2
11 9 12 7 10 5 8 3 6 1 4 2
9 11 7 12 5 10 3 8 1 6 2 4
9 7 11 5 12 3 10 1 8 2 6 4
7 9 5 11 3 12 1 10 2 8 4 6
7 5 9 3 11 1 12 2 10 4 8 6
5 7 3 9 1 11 2 12 4 10 6 8
5 3 7 1 9 2 11 4 12 6 10 8
3 5 1 7 2 9 4 11 6 12 8 10
3 1 5 2 7 4 9 6 11 8 12 10
1 3 2 5 4 7 6 9 8 11 10 12
1 2 3 4 5 6 7 8 9 10 11 12
They even tried to find a solution for fifteen bells, but because it is an odd number of bells they weren't able to stick to the rule that on alternate rows we swap all of the bells (in pairs) and on the remaining rows, we fix the bells on either end and swap the rest.
Teachers' Resources
