Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Move a Match
Age 7 to 11
Challenge Level 





Take $10$ matchsticks and put them into four piles.
For example, you could have a pile of $1$, two piles of $2$ and a pile of $5$:
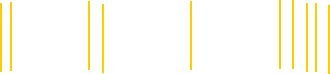
Now, the idea is to take one matchstick from each of three of the piles and add it to the fourth.
So, for example, we could take one stick from the two piles of $2$ and one from the pile of $5$ and add them to the pile of $1$. This would give:

So now we have two piles of $1$ and two piles of $4$.
We have gone from piles of $2, 2, 1, 5$ to piles of $1, 1, 4, 4$.
How could you put the $10$ matches in four piles so that when you move one match from three of the piles into the fourth, you end up with exactly the same distribution of matches in four piles as when you started? (In other words, in the case above we would have gone from $2, 2, 1, 5$ to $1, 5, 2, 2,$ for example - although this isn't possible!)
What can you say about this starting arrangement of the matches?
Could you arrange, for example, $14$ matchsticks in such a way as to be able to make it work too?
How about $18$ matches?
In general, what can you say about the way in which you must arrange the matchsticks for this to be possible?

