Three way split
Problem
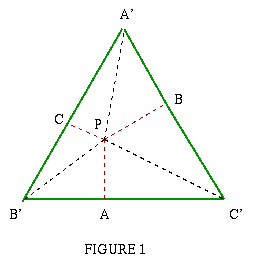
Take any point P inside an equilateral triangle. Draw PA, PB and PC from the point P perpendicular to the sides of the triangle where A, B and C are points on the sides. Prove that the sum of the lengths PA + PB + PC is a constant.
Suppose there is an election with only 3 parties. Draw a diagram on which you can mark a point to show the percentage of winning candidates from each party. (This could be used on the night of the election, moving the point as the results for the different seats come in, showing how well each of the parties are doing overall). Shade the regions where one of the parties has a clear majority and a region where there is no overall majority.
Student Solutions
Image
Image
PA, PB and PC are the heights of triangles PB'C', PC'A' and PA'B'. If the length of the side of the equilateral triangle is L units, then: Area PA + PB + PC = (2 x Area |
Image
|
| For each position of the point P inside
the equilateral triangle we can take PA, PB and PC to represent the
percentages of something which is split into three parts, the total
being represented by PA +PB +PC . As P moves closer to A' the
length PA increases and when P coincides with A' we have PB = PC =
0. We can label the vertices of the triangle to represent the three
parts so that PA gives the percentage of A', PB gives the
percentage of B', and PC gives the percentage of C'. Suppose, for
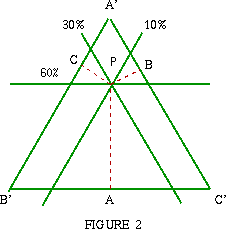
example, these percentages are 60%, 30% and 10% respectively. If we
draw an equilateral triangle with sides of length L = 200/
Image
|
|
| To find the position of P draw lines parallel to the sides of the triangle as shown in the diagram such that anywhere on the 60% line the perpendicular distance between this line and the line B'C' = 60 so PA = 60, similarly the distance between the 30% line and the line C'A' is 30 units so that PB = 30, and the distance between the 10% line and the line A'B' is 10 units so that PC = 10. Because PA + PB + PC = 100 (as we have shown) these three lines intersect in a single point. | Image
|
| We apply this to the percentage of
votes given to three parties A', B' and C' in an election (where
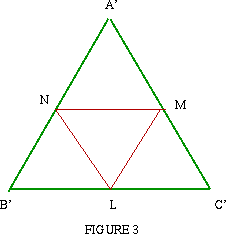
there are no other candidates.) Points L, M and N are the midpoints
of the sides of Image
If the point P lies on NM then height PA is half the height of
Similarly, if P is inside |
Image
|
