Chess
Problem
Place a Knight from a chess set on the corner of a 3 by 3 square board:
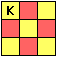
It would need 4 usual Knight's moves to place it in the opposite corner. One possible set of moves is shown below:
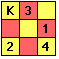
- What would be the smallest number of moves needed to move from
one corner to the opposite corner of a 99 by 99 square board?
- What would be the smallest number of moves needed to move from
one corner to the opposite corner of an n by n
square grid?
Student Solutions
This is an interesting investigation with many possible ways of solving and generalising the problem, and several people wrote in giving an answer of 66 moves.
Isabelle from Lathallan School investigated what happened with different sized grids, and spotted a pattern, which she used to get an answer of 66.
The smallest numbers of moves for 99 squares is 66 moves. I worked out the smallest number of moves for a 3 square grid which was 4. I then worked out the number of moves for a 4 square (which was 2) and a 5 square which was 4. The 6 square was also 4 and so was the 7 square. And then because the moves have to go from a white square and end up on a white square then the number of moves cannot ever be an odd number. So then I tried 8, 9 and 10 square grids which all needed6 moves. So then when I got to 15 squares I needed 10 moves. So then I worked out that a 30 square needs 20 moves. The number of squares is 1.5 times the number of required moves. I tested this at 45 squares (30 moves) and therefore at 99 squares it was 66 moves.
Emily from Durham Johnston Comprehensive School and Tom from Bristol Grammar School both used algebra to explain Isabelle's pattern. Here is Tom's solution:
