Two Ladders
Two ladders are propped up against facing walls. At what height do the ladders cross?
Problem

The picture shows two ladders propped against facing walls. The end of the first ladder is $5\text{m}$ above the base of the second wall. The second ladder is $5\text{m}$ above the base of the first wall.
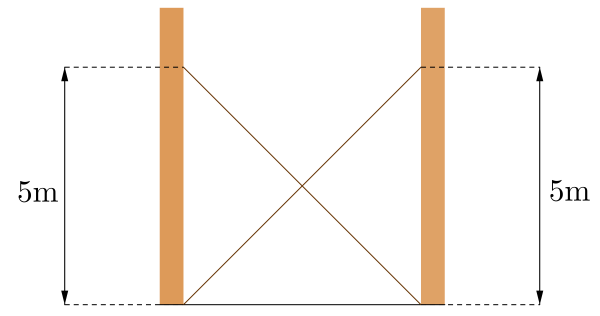
Can you work out at what height the ladders cross?
Are you surprised that we don't need to know the distance between the two walls?

Suppose now the first ladder is $10 \text{m}$ above the base of the second wall, with the second ladder remaining as before.
Can you work out at what height the ladders cross now?
Click below to reveal a diagram that may help you get started:
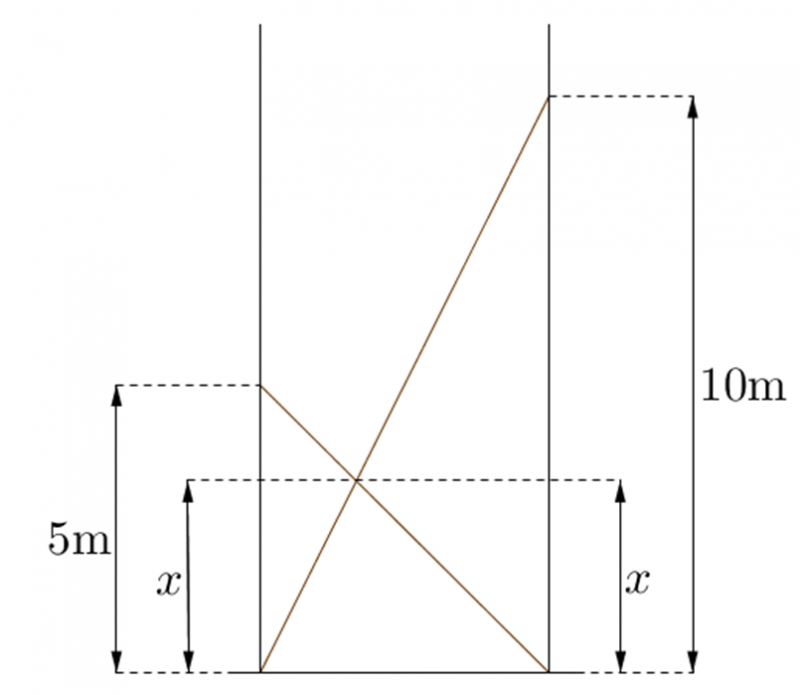
Can you find any pairs of similar triangles in this diagram?
How do these help you to find the value of $x$?
Suppose the first ladder meets the wall at a height of $a$ metres, as in the diagram below.

At what height do the ladders cross now?
Suppose the second ladder meets the wall at a height of $b$ metres, as in the diagram below.
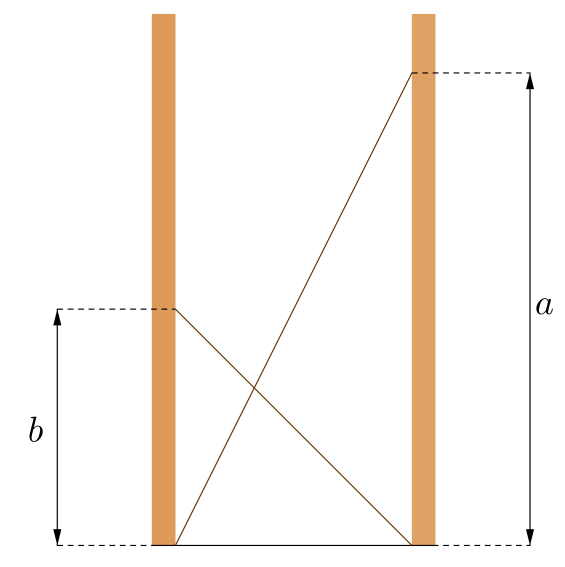
At what height do the ladders cross now?
Explain how you worked out your answer.
Student Solutions
Rhiannon sent in this excellent solution:
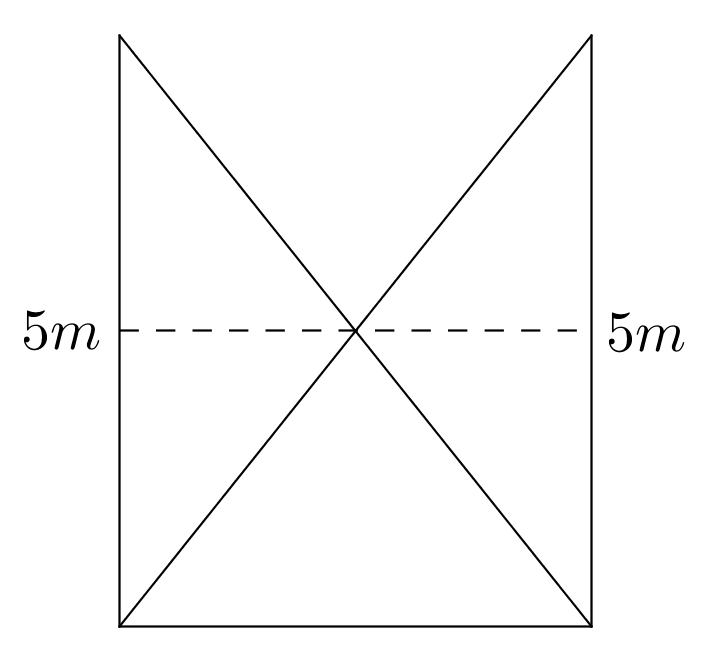
When the ladders both have their tops $5m$ above the ground, the diagram has a line of symmetry, shown in the first diagram as a dotted line, since the ladders both start and end at the same height.
This means the point of intersection must be halfway between the bottom and the top of each of the ladders, and therefore must be $2.5m$ above the ground.
I expected to need to know how far the bases of the ladders were apart, so not needing to know this surprised me.
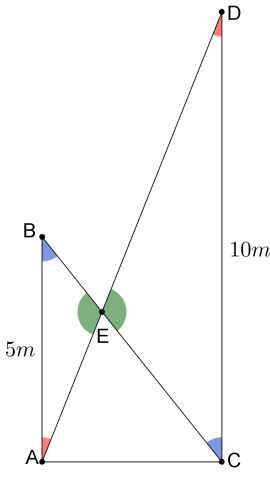
When the second ladder is $10m$ above the ground, I used a different approach. Since both the walls are perpendicular to the ground, they must be parallel.
This tells me that the angles $\angle BAD$ and $\angle ADC$ are alternate angles, and therefore equal. Likewise, angles $\angle ABC$ and $BCD$ are also alternate and therefore equal.
$\angle BEA$ and $\angle CED$ are opposite, which means that they are equal. You can see these equal angles in the diagram on the right.
This means that the triangles $ABE$ and $DCE$ have the same angles as each other, and are therefore similar.
This means:$$\frac{AE}{ED}=\frac{AB}{DC}=\frac{5m}{10m}=\frac{1}{2}$$
Therefore $AE = \frac{1}{3}AD$.
This means $E$ is $\tfrac{1}{3}$ of the way up from the floor to $D$, so is at a height of $\frac{10m}{3}=3\tfrac{1}{3}m$
If instead $B$ is $a$ metres above the floor, then:$$\frac{AE}{ED}=\frac{AB}{DC}=\frac{a}{10}$$Therefore $AE = \frac{a}{10+a}AD$.
This means $E$ is the same fraction of the $10m$ above the floor, so is $\frac{10a}{10+a}$ metres above the floor.
If instead $D$ is $b$ metres above the floor, then:$$\frac{AE}{ED}=\frac{AB}{DC}=\frac{a}{b}$$Therefore $AE = \frac{a}{a+b}AD$.
This means $E$ is the same fraction of the $b$ metres above the floor, so is $\frac{ab}{a+b}$ metres above the floor.
Teachers' Resources
This printable worksheet may be useful: Two Ladders
Why do this problem?
In this problem, students can explore how to find the point where two ladders leaning against different walls cross each other. The problem begins with a special case where symmetry can help and then presents several other more general cases. Students will have plenty of opportunity to work with similar triangles and ratios and may also make connections between the general and particular cases.
Possible approach
Start by asking students to observe the diagram and explain that it represents the two ladders leaning against two walls.
What shapes do they see?
What can they say about the lines that represent the walls?
How are the angles in the diagram related to each other?
If students mention symmetry or similar or congruent triangles, make a note of this but otherwise wait to see if students mention these later.
Now ask students to think about how they could find the height of the point where the ladders cross. Encourage students to work in pairs or small groups and share their ideas. Also encourage them to distinguish between what they know from the geometry of the diagram and any conjectures they have, e.g. about the ladders meeting half way up.
Encourage students to draw the diagram for themselves and add what they know about the lines and angles.
Once groups have found an answer, ask them to justify their method. Can they explain their method in a way that makes their reasoning clear?
The second and later problems can be used to consolidate methods and refine reasoning from the first. As students move to these problems, ask them to think again about the points they raised about the first case. Which of these still hold now the ladders are different heights? This could help them to see how these cases generalise from the particular case they’ve already solved, so they might be able to adapt their method rather than starting each case from scratch. Similarly, having solved one of the later problems, encourage students to check whether their answers from their previous special cases agree with their more general result.
Once several groups have made good progress on at least the first two problems, bring the class together to share their methods. Alternatively, you might want to ask students to make simple posters explaining their reasoning.
Key questions
What shapes can you see in the diagram?
What do you know about the walls?
How are the angles in the diagram related to each other?
How are lengths in the diagram related to each other?
What does it mean for two triangles to be similar?
Is there another way of proving their result?
Possible support
Students could draw the diagram on mini whiteboards and mark in the angles. Remind them that the walls are vertical, so these lines are parallel. Students might find it helpful to draw just one ladder initially and think about the angles it makes with the two walls.
You could also ask students about what they know about similar triangles and how they could apply this to their diagram.
To support students with the second part of the problem, you could share this diagram:

As students if they can find any pairs of similar triangles in this diagram? How do these help them to find the value of $x$?
Possible Extension
Students could go on to Nicely similar or Two Trees.
