STICKS and Triangles
Problem
I made some triangles out of sticks. The sticks are all the same length.
I can make a triangle out of three sticks:
What about four sticks? Five sticks? Six sticks?
I can make two different triangles out of ten sticks:
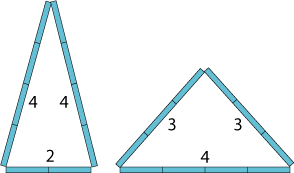
Can you find any others?
What about triangles made from twenty sticks?
What about all the lengths in between?
Can you make any rules about the numbers of sticks that make the most triangles?
Getting Started
Have you got some headless matches or lolly sticks or straws that you could use to try out your ideas?
Whatever number of sticks you are trying, it might be a good idea to start by trying to make a triangle which has just one stick as a side.
Can you make any triangles with a side of two sticks? How about three sticks? Four? ...
Student Solutions
This fun problem encouraged you to work systematically, and develop a way to record and organise your findings. For some numbers of sticks, there are several different possibilities, so it is important to approach the problem carefully, to ensure all of the options are explored.
Cong from St Peter's Roman Catholic School, Aberdeen was very thorough indeed, and sent in a fantastic solution to this problem. You must have worked very hard, Cong!
Cong sent us a table of all the different triangles you can make with 4 sticks up to 20 sticks. Making a table was a very good idea. However, it's a bit long to put on a webpage, so I've made a list of all the triangles in Cong's table so you won't have to scroll too far to read them all!
Four sticks - noneFive sticks -2, 2, 1
Six sticks - 2, 2, 2
Seven sticks -3, 3, 1 and 3, 2, 2
Eight sticks -3, 3, 2
Nine sticks - 4, 3, 2 and 4, 4, 1 and 3, 3, 3
Ten sticks - 4, 4, 2 and 4, 3, 3
Eleven sticks - 5, 5, 1 and 5, 4, 2 and 5, 3, 3 and 4, 4, 3
Twelve sticks - 5, 5, 2 and 5, 4, 3 and 4, 4, 4
Thirteen sticks - 6, 6, 1 and 6, 5, 2 and 6, 4, 3 and 5, 5, 3 and 5, 4, 4
Fourteen sticks - 6, 6,2 and 6, 5,3 and 6, 4,4 and 5, 5, 4
Fifteen sticks - 7, 7, 1 and 7, 6, 2 and 7, 5, 3 and 7, 4, 4 and 6, 6,3 and 6, 5, 4 and 5, 5, 5
Sixteen sticks - 7, 7, 2 and 7, 6, 3 and 7, 5, 4 and 6, 6, 4 and 6, 5, 5
Seventeen sticks - 8, 8, 1 and 8, 7, 2 and 8, 6, 3 and 8, 5, 4 and 7, 7, 3 and 7, 6, 4 and 7, 5, 5 and 6, 6, 5
Eighteen sticks - 8, 8, 2 and 8, 7, 3 and 8, 6,4 and 8, 5, 5 and 7, 7, 4 and 7, 6, 5 and 6, 6, 6
Nineteen sticks - 9, 9, 1 and 9, 8, 2 and 9, 7, 3 and 9, 6, 4 and 9, 5, 5 and 8, 8, 3 and 8, 7, 4 and 8, 6, 5 and 7, 7, 5 and 7, 6, 6
Twenty sticks - 9, 9, 2 and 9, 8, 3 and 9, 7, 4 and 9, 6, 5 and 8, 8, 4 and 8, 7, 5 and 8, 6, 6 and 7, 7, 6
Cong has made each triangle in turn in a very systematic way. Can you see how Cong has started with the longest side possible each time and worked down? He always lists the side lengths with the longest first as well. This makes it very easy to check. Well done!
Cong summarised the number of possible triangles with each number of sticks in another table:
| Number of sticks | Number of triangles |
| 3 | 1 |
| 4 | 0 |
| 5 | 1 |
| 6 | 1 |
| 7 | 2 |
| 8 | 1 |
| 9 | 3 |
| 10 | 2 |
| 11 | 4 |
| 12 | 3 |
| 13 | 5 |
| 14 | 4 |
| 15 | 7 |
| 16 | 5 |
| 17 | 8 |
| 18 | 7 |
| 19 | 10 |
| 20 | 8 |
He also showed the same information on a bar chart. Notice that there are no possible triangles with four sticks. Holly from Anston Brook Primary School said:
Children from Riversdale Primary School examined the "rules" for the longest side of any triangle:
Well done for spotting this. Can you see why this is the case? This is actually an example of the "triangle inequality". Do not worry, this sounds more difficult than it is! The triangle inequality applies to any triangle, and states that the length of a given side must be less than or equal to the sum of the two other sides. So, imagine that you have a triangle with sides of three, four and five. The longest side, five, is less than the sum of the two other sides ($3+4=7$). So, this is an example of the triangle inequality in action!
What does this mean for the problem with sticks? Well, firstly it provides a quick way to check if the triangles you have thought about are possible. Secondly, it can also save you some time when working out all of the possibilities. For example, you may be able to see that, for this task with sticks, the triangle inequality means that the length of any side cannot be greater than half of the total number of sticks. If the length of a side used is more than half of the total number of sticks, this would not agree with the triangle inequality, and a triangle could not be made. Why not have a go at this to see for yourself to check you understand why the triangle inequality is true?
Cong also spotted a general "rule":
Yes, I see what you mean, Cong. Children from Riversdale Primary School also submitted a similar table. They also made a similar observation:
Odd numbers of seven and above always have more triangles than the even numbers adjacent to them. Odd numbers in the three times tables have even more as they have an equilateral triangle as well.
In addition, Ellie, Emma, Olivia and Ibrahim from Lakeside looked at "rules" for being able to make equilateral triangles:
Well done for these fantastic solutions and observations!
Teachers' Resources
Why do this problem?
Possible approach
You could start by showing the problem as it is given from a computer or print out of the text. Alternatively, you could hand out sticks and ask the group what is the least number of sticks they will need to make a triangle. Then ask them to see if they can make a triangle with four sticks. It might be a good idea at this point to make quite sure that all the group know that a triangle has three straight sides!
At the end there should be time to discuss their findings. Ask them for which numbers of sticks did they find the most triangles? Can they think why this should be so?
Things to draw out from this activity include:
Key questions
How are you going to record your findings?
Are you sure you have found all the possible triangles with that number of sticks?
Whatever number of sticks you are trying, it would it be a good idea to start by trying to make a triangle which has just one stick as a side.
How many sticks have you along the base of that triangle?
Could you try another number of sticks along the base?
Can you see any differences between odd and even numbers of sticks?
What about looking at numbers of sticks which are multiples of three?
Possible support
Suggest that learners who find this problem difficult work steadily with real sticks starting with triangles with three sticks and working upwards. Drawing what they have done is probably the easiest way to record but it might be helpful to show them how a table can be made of their results. It may be helpful for children to have had a go at the task Let's Investigate Triangles as a precursor to this one.
Possible extension
Learners could make a table of results and formulate any 'rules' for when it is possible to construct a triangle and when it is not possible. They could then predict the numbers of triangles they should be able to make for 21 to 30 sticks and then test their predictions.
