Clock Hands
This investigation explores using different shapes as the hands of the clock. What things occur as the the hands move.
Problem
I've been wandering around the shops where I live in Cambridge - there are a lot of shops that seem to be selling interesting looking watches and clocks. Some challenges on NRICH are about digital numbers but lots of people like to use an analogue clock or watch instead. ('Analogue' for our use, means that it is not digital and has a round face with two hands and twelve numbers!)
Well, there are some fascinating ideas. I have a clock in which the hands go around anticlockwise and so do the numbers! There are so many designs, perhaps you've seen some and have been fascinated by them.
I was wondering about different shaped hands. How about a pair of square hands, but we will tilt each hand 45 degrees so that the corner points and the opposite corner is in the centre. I've tried drawing some of these ideas. (However I have not allowed the hour hand to move and the hour is 12, it's only the minute hand that's moving at the moment!). To help to understand the pictures I placed a little dot where the hands are pointing.
So at 12 o'clock it would look like this:-

Every ten minutes later (Remember that I'm not allowing the hour hand to move) we'll have:-
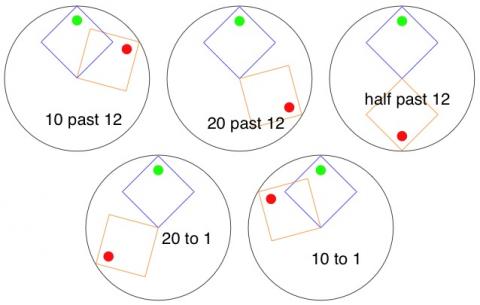
I like the overlap shapes that have been formed.
You could try this with paper squares or coloured see-through sheets and a pin stuck very, very close to the corner that's pretending to be the middle of the clock face.
Have a go and see what things occur as the minute hand moves and you hold the hour hand still, look at shapes of overlap and a sort of "Jaw" shape that opens and closes.
We should be used to asking "I wonder what would happen if ...?''
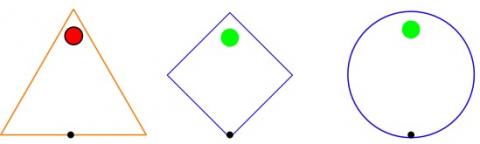
As you can guess I do this frequently and so I used my computer to help me with an equilateral triangular one. Here they are:-
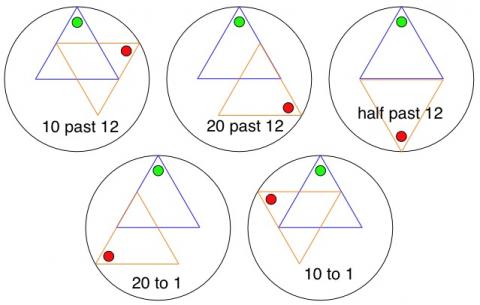
Of course why should we stop there? Circles!:-
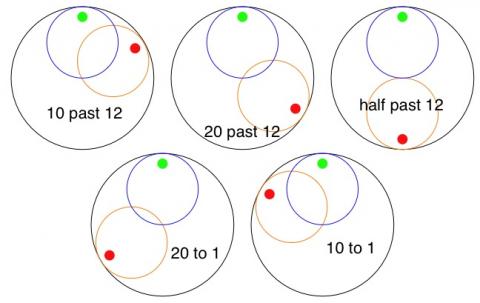
You can try and explore all different designs. You don't have to just look at the position every ten minutes like I have done; you could try any minutes past/to that you liked.
If you are the sort of person who prefers to work with a clock that the hour hand moves properly with the minutes hand then you might like to look at these:-
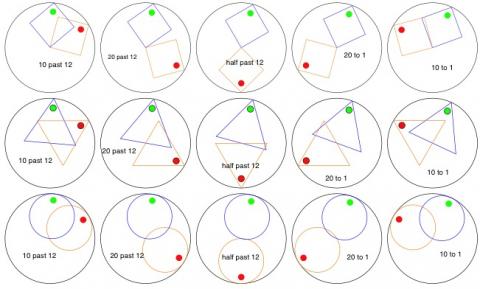
Good luck.
Getting Started
You could cut out hands from coloured tissue paper or coloured overhead transparencies so you can see the overlap better.
Student Solutions
It seems that everyone found this a bit tough! It certainly is very hard to picture the shapes moving around. You really need to find some clear plastic to draw the shapes on, so you can turn them around and see what happens. Or, you could just cut some out of cardboard. You might try drawing them on thin paper and holding them up on a window to let the light shine through.
Try one of these ways of making the clock hands and have another go at the investigation. We would be thrilled to get some solutions on this one.
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
Possible support
