You may also like

Geoboards

This practical challenge invites you to investigate the different squares you can make on a square geoboard or pegboard.

Tiles on a Patio

How many ways can you find of tiling the square patio, using square tiles of different sizes?

Pebbles

Place four pebbles on the sand in the form of a square. Keep adding as few pebbles as necessary to double the area. How many extra pebbles are added each time?

Torn Shapes

Age 7 to 11
Challenge Level

Torn Shapes


Jason's class cut out rectangles and some shapes which were two rectangles joined together from one centimetre squared paper.
They then counted how many squares the shapes took up.

After this they tore a piece out of some of their shapes to make a puzzle for the other groups to do.
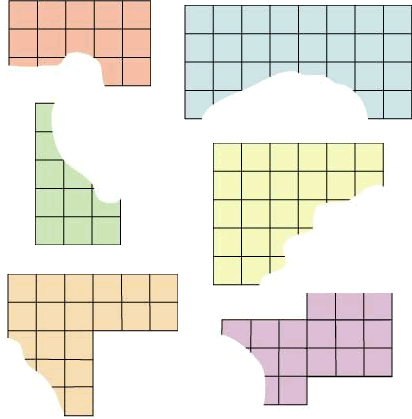
Can you work out how many squares there were in these shapes before the bit was torn out? The orange, blue, green and yellow shapes were rectangles. The bottom two shapes, which are pale orange and purple, were each two rectangles joined together.
 
six torn rectangles
Courtney's group tore too much off their grey rectangle!
 
torn rectangle
 
What is the smallest number of squares it could have had?
What is the largest number of squares it could have had if it was not longer than any of the other shapes?

 

Why do this problem?

This problem is a good way to assess children's understanding of properties of rectangles. The problem is a nice lead into area, although this is not specifically mentioned in the wording. Torn Shapes is a challenge that encourages children to adopt a different technique for finding area rather than simply counting squares.

 

 


Possible approach

 

You could introduce these ideas by drawing a torn shape of your own, or cutting out a shape and then tearing it (perhaps part of a square or a triangle), and asking the children to decide how many small squares it takes up. This might involve you asking the group for suggestions as to how they might go about solving the problem, and probably modelling these for them.

 

After this you could show the group the actual problem on an interactive whiteboard or data projector. Then they could work on it in pairs with the shapes from this sheet or on screen with access to squared paper. It is important to allow plenty of time for children to share their thinking and explanations with their partners and the rest of the group. Some children might want to count each square individually, but that is difficult with this problem. Others might count a row or column and use their knowledge of multiples. It is likely that they will spend some time discussing how best to approach this problem before reaching that conclusion.

 

 

As a plenary activity, you could have a torn piece of squared paper which is ambiguous in terms of the original shape it came from and use this to discuss the possible numbers of squares it contains. There is no reason why you should not make your own torn shapes from squared paper using the activity as an idea rather than a problem to be solved.

 

 

Key questions

 

How many squares are there in a row that is complete?

How many rows are there altogether whether they are complete or not?


Possible extension

You could change the last part of the question so that, rather than it being no longer than any of the other shapes, the final shape has no more than 100 squares. Can learners find all the possible solutions? Challenge them to articulate the pattern in the answers.


Possible support

Children would benefit from trying Wallpaper first.

 

 

 

The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice.
Copyright © 1997 - 2023. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.