You may also like

Three Cubes

Can you work out the dimensions of the three cubes?

Nine Colours

Can you use small coloured cubes to make a 3 by 3 by 3 cube so that each face of the bigger cube contains one of each colour?

Marbles in a Box

How many winning lines can you make in a three-dimensional version of noughts and crosses?

Cubic Covering

Age 14 to 16 Short
Challenge Level
We first imagine the cross with the blue cubes only:
 

We now glue the yellow faces to the up and bottom faces of the blue cross. We require 5 yellow cubes for wrapping each of the two blue cubes. (We used transparent yellow cubes)
 
        

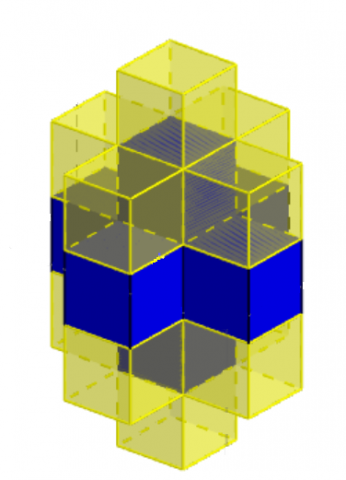
Now we need one yellow cube for each of the four corners:
Finally, we have 4 faces to cover, so we need 4 more squares.

Therefore, we used $5+5+4+4 = 18$ yellow cubes.
 

This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice.
Copyright © 1997 - 2023. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.