Fermat's Poser

To find the point, try the following experiment:

The Thought Experiment

Consider any triangle where the angles are all less than 120 degrees. Imagine 3 pieces of string of equal length and knot them together so that the 3 trailing ends are of equal length. Imagine a tiny hole at each vertex of the triangle and thread the ends of the string through the 3 holes. Attach 3 equal weights to the ends and support the triangle horizontally so that the weights hang down freely. What happens to the knot?

Continuing the 'thought experiment': The knot slides across the triangle until the system settles down in equilibrium with the tension in all three strings equal. Because of these equal tensions the angles between the 3 strings must all be 120 degrees. Because the weights will drop as low as they can the sum of the lengths of the hanging pieces of the strings will be a maximum and the sum of the lengths of the pieces from the knot to the vertices will be a minimum (minimising the potential energy of the system).

For triangles where the biggest angle is 120 degrees or more the knot will settle at the vertex with the obtuse angle.

To construct the point draw an equilateral triangle on each side of the original triangle ABC and then join the outer vertices of the equilateral triangles to the opposite vertices of the original triangle and you will find that these three lines are concurrent (i.e. they all go through one point). Label this point O. You will find that the angles between OA and OB, between OB and OC and between OC and OA are all 120 degrees. The proof of these facts follows.

Constructing the point

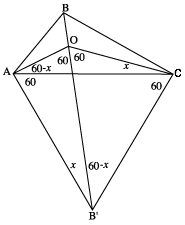
1.	Consider any triangle ABC.
2.	Draw an equilateral triangle AB'C with B' on the opposite side of AC to B.
3.	Join BB'.
4.	Draw CO with point O on BB' and angle ACO = angle AB'O =x
5.	Note angle COB' = 60 because the other two angles of triangle COB' are (60 + x ) and (60 - x ).
6.	We now see that angle B'OC = angle B'AC = 60 so the quadrilateral AOCB' is cyclic (see the article on cyclic quadrilaterals).
7.	Hence angle AOB' = angle ACB' = 60 .
8.	As BOB' is a straight line, angle AOB = angle BOC = angle COA = 120 .
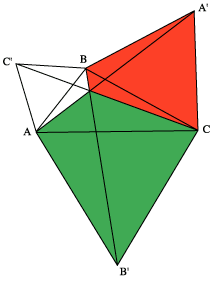
9.	A similar argument shows that when equilateral triangles CA'B and BC'A are drawn on the other two sides of the original triangle, two further cyclic quadrilaterals CA'BO and BC'AO are formed.