Maximum Scattering
Your data is a set of positive numbers. What is the maximum value
that the standard deviation can take?
Problem
Image
|
a) The data obtained from a given experiment is a pair of
numbers $a$ and $b$, where $a\geq 0$ and $b\geq 0$. It is known
that $a$ and $b$ have mean $1$; what is the largest value that the
standard deviation can be?
(b) The data obtained from a given experiment is a triple of
numbers $x$, $y$ and $z$, where each is non-negative. It is known
that the mean of $x$, $y$ and $z$ is $1$; what is the largest value
that the standard deviation can be?
|
(c) The data obtained from a given experiment is a set of numbers $t_1,\ldots,t_n$, where each is non-negative. It is known that the mean of the $t_j$ is $1$. Show that the standard deviation may be as large as $\sqrt{n-1}$.
Getting Started
To work out the variance you have to sum the squares of the
differences of all the numbers from the mean.
To do this question you could think of the set of numbers as a point in space and use geometrical reasoning to help you to decide which position(s) of the point gives the greatest variance. A 'special' point occurs where all the numbers in the set are equal to the mean. Can you see how the variance for any set of numbers relates to the distance of the corresponding point from the 'special' point?
The constraints that the mean of the numbers is given, and that the numbers are all positive, restrict the points to lie in a certain region.
To do this question you could think of the set of numbers as a point in space and use geometrical reasoning to help you to decide which position(s) of the point gives the greatest variance. A 'special' point occurs where all the numbers in the set are equal to the mean. Can you see how the variance for any set of numbers relates to the distance of the corresponding point from the 'special' point?
The constraints that the mean of the numbers is given, and that the numbers are all positive, restrict the points to lie in a certain region.
Student Solutions
Ruth from Manchester High School for Girls sent us her work on this problem. Well done, Ruth!
(a) When there are $2$ numbers,
their total is $2$. The possibilities for the values of the two
numbers can be represented as a straight line $x+y=2$ on a graph.
The mean is the point $(1,1)$ in the centre of the line. The
standard deviation ($\sigma$) is greatest when the distance between
the values and the mean is largest. The endpoints are furthest from
the centre so $\sigma$ is largest at the point $(2,0)$ when it is
equal to $1$.
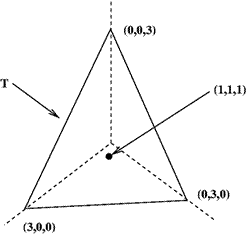
(b) When there are $3$ values,
their total is $3$. This is represented by a plane. As the numbers
are non-negative the only values for the numbers are in a triangle
with the corners at $(0,0,3)$, $(0,3,0)$ and $(3,0,0)$. These are
the points furthest away from the mean which is at $(1,1,1)$ so are
where $\sigma$ is greatest and it is $\sqrt{2}$.
(c) When there are $n$ values, the
total is $n$. The region where this is true and they are
non-negative is a $n-1$-dimensional shape with $n$ corners which
have coordinates $(0,0,...,0,n)$ each with the $n$ in a different
position and $n-1$ $0$s. These are furthest from the mean (which is
at $(1,1,...,1,1)$) so are where the value of $\sigma$ is greatest.
$\sigma$ is the square root of the difference between the square of
mean and the mean of the squares. The mean is $1$ so the mean
squared is $1$. The squares are $n^{2}$, 0, 0, ... so the total of
the squares is $n^{2}$ and their mean is $n$. This makes $\sigma=
\sqrt{n-1}$.
In fact, as is explained in the
notes , we'd have to do some geometry for (c) to prove that the
points are indeed the furthest from the mean. But for this question
all we are asked to do is to show that the standard deviation can take a certain value, and Ruth
has done this.
Teachers' Resources
Having done the first two parts of the question you can show similarly that, with $n$ numbers, there exists a certain value of the variance and hence that the variance can be at least that large. It is quite a subtle point, but you can't be sure that you have found the largest value of the variance with $n = 4$ or more without assuming that the geometrical reasoning generalises from $3$ dimensions to higher dimensions. The results are in fact valid in $n$-dimensional geometry but you are not asked to prove this.
