Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Published 2006 Revised 2022
Back to the Practical?
When you are working your way, with the youngsters, through a long investigation it can be extremely useful to see how certain people work - their route - if you like. I've found that one very healthy route has been something like this, for example, when working on The Big Cheese:
- Start with practical - get results from the first block.
- Explore other blocks and then realise you are covering very similar, if not the same, results.
- Ask questions like:
-
- what about the surface area of the slices?
- what about the surface area of the remaining block after each cut?
- what about the sizes of all the eventual slices?
- Tabulate the results - from simply writing them down in a line to sophisticated spreadsheets.
- Explore the things in the table. This is where you are really having a new branch of the investigation by exploring a set of numbers from the table in their own right - probably forgetting where they've come from.
For example,
You may look at the sizes of all the slices that came from the $5$ by $5$ block: $1, 1, 2, 4, 4, 6, 9, 9, 12, 16, 16, 20, 25$.
So we move from the arithmetic exploration to playing around with the practical again.
I shall show the practical in diagrammatic form:
Here we have the $9$ and the $12$ slices.
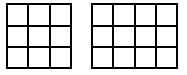

So the $9$ and the $12$ happily went together to form $21$ - a triangular number!
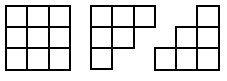
Now let's try the same with the $12$ and the $16$. Here are the four stages.

Appreciating this practically helps many pupils to gain a better realisation of the relationship between these two sets of numbers.
Having come away from the table of results and explored some relationships practically we could end there, BUT if the group have an opportunity to go back then, with greater confidence now, they can ask further questions. I would recommend that you invite the youngsters to ask the kind of questions that would lead to more exploration, more calculations AND maybe back to the practical again. An
example might be;
"What's the surface area when we start with a $5$ by $5$ by $5$ cube?" [$150$]
"After the first slice [a $5$ by $5$ by $1$] is taken, what's the total surface area of the two pieces?"
[Well the starting cube is now only $5$ by $5$ by $4$ and so has a surface area of $130$ and the slice is $5$ by $5$ by $1$ and so has a surface area of $70$, giving a total of $200$! $\ldots$]
Sometimes when doing investigations we are very practical and find all we need to without having to go into complicated arithmetic. BUT what happens when trying the Brush Loads investigation?
Suppose you go along the route of finding the smallest surface areas for different numbers of cubes. The discovery is usually made - see the teachers' resources for the activity - that the shapes have to be flat. So let's look at some of the answers shown in plan view:
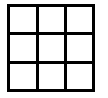
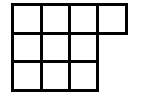
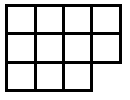
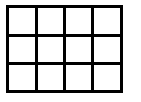
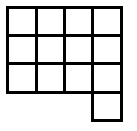
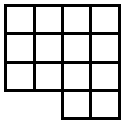
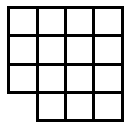

Now, as mentioned in the notes for this activity, children count the squares on the surface in different ways. Those who settle for viewing from the four sides and then adding the top sometimes have found out that they only have to consider, in these examples, two adjacent sides. The two adjacent sides are viewed and then added and doubled. Finally the number on the top - the number of cubes -
is added on.
Looking at the examples above we have:
10 cubes give 3 + 4 doubled + 10 = 14 + 10 = 24
11 cubes give 3 + 4 doubled + 11 = 14 + 11 = 25
12 cubes give 3 + 4 doubled + 12 = 14 + 12 = 26
13 cubes give 4 + 4 doubled + 13 = 16 + 13 = 29
14 cubes give 4 + 4 doubled + 14 = 16 + 14 = 30
15 cubes give 4 + 4 doubled + 15 = 16 + 15 = 31
16 cubes give 4 + 4 doubled + 16 = 16 + 16 = 32
Now the patterns and arithmetic can be explored further according to the interests of the youngsters involved. I could imagine some pupils being able to talk about a sort of 'formula' that would represent a generalisation.
So let's be clear that when working practically we may need to explore what's going on arithmetically and when working arithmetically we may need to explore what's going on practically.
Here is a PDF version of this article.

