Gold yet again
Nick Lord says "This problem encapsulates for me the best features
of the NRICH collection."
Problem
Nick Lord says that this problem is immediately enticing for students (and for him) and there are many possible approaches to explore and compare.
Image
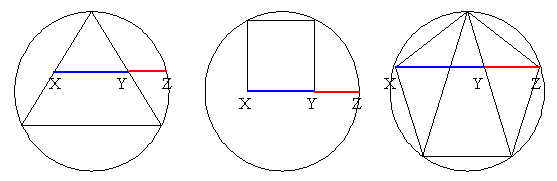
In the equilateral triangle inscribed in the circle, $X$ and $Y$ are the midpoints of the edges. Find the ratio${XZ\over XY}$.
The square sits on a diameter of the circle. Find the ratio ${XZ\over XY}$.
The regular pentagon is inscribed in the circle. Find the ratio ${XZ\over XY}$.
See also the problem Gold Again.
Getting Started
In the equilateral triangle, draw in the altitudes of the triangle
and taking the radius of the circle as $1$ unit, calculate the
lengths.
In the square it is easiest to take the side of the square as $1$ unit and then calculate the radius of the circle.
In the pentagon it is easiest to take the side of the pentagon as $1$ unit, and the chord length $XZ$ as $x$ units and then use properties of similar triangles. Derive a quadratic equation which you can solve to find $x$.
In the square it is easiest to take the side of the square as $1$ unit and then calculate the radius of the circle.
In the pentagon it is easiest to take the side of the pentagon as $1$ unit, and the chord length $XZ$ as $x$ units and then use properties of similar triangles. Derive a quadratic equation which you can solve to find $x$.
Student Solutions
Thank you to Lazarus from Colyton Grammar School and Andrei from Tudor Vianu National College, Bucharest for your solutions to this problem. We see that in all three cases the ratio $XZ$ to $XY$ is the Golden Ratio.
Image
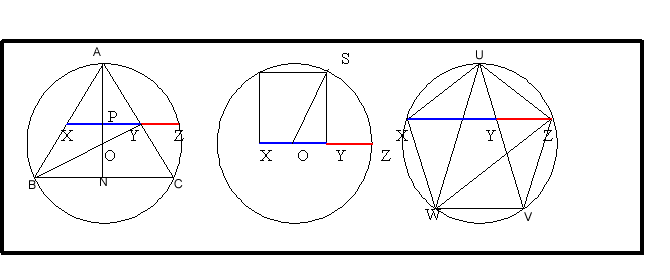
In the first diagram, taking the circle to have unit radius, $AO = BO = CO = ZO$.
Triangle $BXO$ is similar to triangle $XPO$ (angles $30^\circ, 60^\circ, 90^\circ$) so $BX = BO\cos30 = {\sqrt 3\over 2}$ and $XO = BO\sin 30 = {1\over 2}$, $OP = XO\sin 30 = {1\over 4}$ and $XP = PY = XO \cos 30 ={\sqrt 3\over 4}$ so $XY = {\sqrt 3 \over 2}$.
Now consider triangle $OPZ$. Angle $OPZ = 90^\circ$. Therefore using Pythagoras' Theorem, $PZ= \sqrt{1 - {1\over 16}}= {\sqrt{15}\over 4}$. So $XZ= XP + PZ = {\sqrt{3}\over 4}\left(1 + \sqrt{5}\right)$ and $${XZ\over XY} = {1\over 2}\left(1 + \sqrt{5}\right)$$ which is the Golden Ratio.
In the second diagram, taking the side of the square $XY$ as $1$ unit and using Pythagoras Theorem for triangle $OSY$ gives $OS={\sqrt 5 \over 2}$ which is the radius of the circle. So $OZ ={\sqrt 5 \over 2}$. Hence $XZ = {1\over 2}\left(1 + \sqrt{5}\right)$ and $${XZ\over XY} = {1\over 2}\left(1 + \sqrt{5}\right)$$ again the Golden Ratio.
In the third diagram take the sides of the pentagon to be $1$ unit long and the chords $XZ$ and $WZ$ etc. to be $x$ units.
Triangles $UXY$, $YVZ$ and $XZW$ are similar isosceles triangles (angles of $36^\circ$, $72^\circ$ and $72^\circ$) with $VY =VZ = XY = 1$ and $YZ = x-1$. We see that the ratio we want to find $XZ/XY = x$.
By similar triangles, taking the ratio of the long to the short sides, we get $${x\over 1 } = {1 \over{x-1}}$$ which gives the quadratic equation $$x^2 - x - 1 = 0$$ with solutions ${1\over 2}\left(1 + \sqrt{5}\right)$ or ${1\over 2}\left(1 - \sqrt{5}\right)$. The latter is negative so does not make sense geometrically so the ratio must be the Golden Ratio: $${1 \over 2}\left(1 + \sqrt{5}\right)$$
Teachers' Resources
Nick Lord chose this problem for the 10th Anniversary Edition of the NRICH website and had this to say about it:
"The equilateral case is genuinely surprising; the square case echoes back through the centuries to Euclid's original construction of the golden section, as does the familiar 'diagonal:side' ratio in the pentagon. I say 'familiar' in that annoying way that teachers often do, forgetting that everyone has to encounter beautiful results like this for the first time and that they will struggle to find them in today's school textbooks. It is fantastic to have such gems collated in such a convenient form in one place - gems which I can customise for my own teaching purposes. For example, adjacent to 'Gold Yet Again' on the menu is 'Pentabuild' so, at the click of a button, I can animate the construction of a regular pentagon and we can hunt for the tell-tale evidence of the golden ratio which we now know is needed to make it work. By the end of all this, my students' mathematics has been enriched, my mathematics has been enriched and I log-off smiling that I have struck 'Gold Again' on the NRICH website! "
This problem gives three examples of the occurrence of the golden ratio.
For the pentagon, the hint suggests you use the similar triangles which have angles $72^\circ, 72^\circ$ and $36^\circ$, one with sides $x$, $x$ and $1$ and one with sides $1$, $1$ and $x-1$. Equating the ratios of corresponding sides of these triangles gives a quadratic equation.
Another method of proving the same result is given in
Pent
There is a related problem called
Gold Again
