Walk the plank
A rectangular plank fits neatly inside a square frame when placed diagonally. What is the length of the plank?
Problem
Image
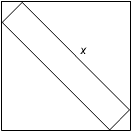
The diagram shows a 1 by x rectangular plank
which fits neatly inside a 10 by 10 square frame.
What is the value of x?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
Image
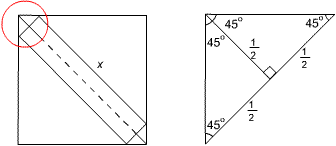
The figure on the right shows the top left-hand corner of the complete diagram. Note the symmetry which leads to the three measurements of $\frac{1}{2}$. Thus the diagonal of the square can be divided into three portions of lengths:
$\frac{1}{2}$, $x$ and $ \frac{1}{2}$ respectively.
The length of the diagonal $= \sqrt{10^2 + 10^2} = \sqrt{200} = 10 \sqrt{2}$.
So $x$ = $10\sqrt{2} - 1$.
