Running Race
Weekly Problem 13 - 2006
If three runners run at the same constant speed around the race tracks, in which order do they finish?
If three runners run at the same constant speed around the race tracks, in which order do they finish?
Problem
Image
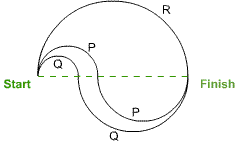
In a leisure park there are three running tracks, all with the same Start and Finish, and all made from either one or two semicircles with centres on the same line.
Three runners $P$, $Q$ and $R$ start together at the Start and run at the same constant speed along the tracks shown. In what order do they finish?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Getting Started
Imagine a circle of diameter $1$ unit, and another circle of a
similar diameter, and another.
What is the total perimeter of these three circles (you can leave your answer with $\pi$ in it)?
What is the perimeter of a circle of diameter $3$ units?
*****
Now imagine two circles - one of diameter $2$ units and one of diameter $3$ units.
What is the total perimeter of these two circles?
What is the perimeter of a circle of diameter 5units?
*****
What do you notice?
Is this generally the case with combinations of circles whose total diameters are equal?
Can you explain why?
What is the total perimeter of these three circles (you can leave your answer with $\pi$ in it)?
What is the perimeter of a circle of diameter $3$ units?
*****
Now imagine two circles - one of diameter $2$ units and one of diameter $3$ units.
What is the total perimeter of these two circles?
What is the perimeter of a circle of diameter 5units?
*****
What do you notice?
Is this generally the case with combinations of circles whose total diameters are equal?
Can you explain why?
Student Solutions
Image

All three runners finish at the same time.
Let the radius of $R$'s track be $r$ and let the radius of the first semicircle of $P$'s track be $p$; then the radius of the second circle of this track is $r-p$.
The total length of $P$'s track is $\pi p + \pi(r-p) = \pi r$, the same length as $R$'s track.
By a similar argument, the length of $Q$'s track is also $\pi r$.
