Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Triangle Midpoints
Age 14 to 16
Challenge Level 





Triangle Midpoints printable sheet
Given the three midpoints of the sides of a triangle, can you find a way to construct the original triangle?
For example:
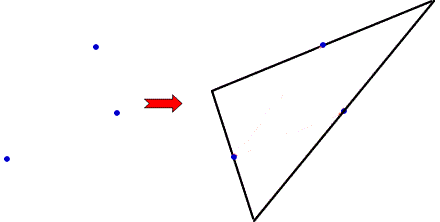
Choose any three points.
Can you construct a triangle such that your three points are the midpoints of its sides?
Is there more than one possible triangle for any given set of midpoints?

