Speeding Up, Slowing Down
Experiment with the interactivity of "rolling" regular polygons, and explore how the different positions of the dot affects its speed at each stage.
Problem
Speeding Up, Slowing Down printable sheet
Take a look at the interactivity below which shows regular polygons "rolling" along the horizontal surface. It leaves a trace of the path of the dot and on the graph it records the speed of the travelling dot.
Experiment by positioning the dot at the centre of the polygons, at one of the vertices or at the centre of one of the sides of the polygons and explore how this affects the speed / time graph.
Challenge:
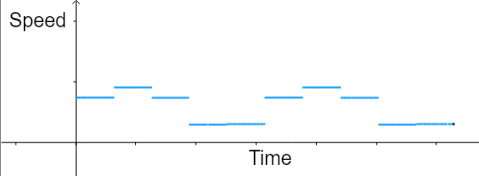
Can you now work out what produced the following speed / time graph?
Can you work out how many sides the polygon had and where the dot was placed?
Try to explain how you worked it out.
Getting Started
Try to approach the problem systematically.
As you go along try to understand why the graph takes the shape that it does:
- by relating it to the rolling polygon and the journey of the dot
- by trying to predict what will happen before you set the polygon rolling
Could the dot have been on the centre of a polygon?
Try for each of the polygons.
Could the dot have been on the centre of the base of a polygon?
Try for each of the polygons.
Could the dot have been on the centre of one of the sloping sides of a polygon?
Try for each of the polygons.
Could the dot have been on the centre of a side opposite the base of a polygon?
Try for each of the polygons.
Could the dot have been on a vertex opposite the base of a polygon?
Try for each of the polygons.
Could the dot have been on a vertex on the base of a polygon?
Try for each of the polygons...
Alternatively...
- try all possible positions of the dot in a triangle,
- and then in a square,
- and then in a pentagon,
- and then in a hexagon...
Student Solutions
Congratulations to those of you who managed to find the right answer.
Robyn from the Katherine Semar Junior School was one of the first to send in a correct answer:
The shape is a pentagon, the dot is on the middle of the bottom left sloping edge.
Robert and Joel from Cowbridge Comprehensive also sent in correct solutions.
Here is Robert's nice piece of detective work:
Since the speed was never zero, the dot could not have been on a corner of the shape, but in the middle of a side.
Robert goes on to consider on which side of the pentagon the dot must have been placed:
Since the line that marked the lowest speed (which was twice as long as the others) was the last line before the graph repeated itself, the dot had to be on the side that came off the ground last.
Therefore, the shape that made that graph was a pentagon, with the dot in the middle of the lower left side.
Thank you Cristina, from City of London School for Girls, for sending us a very comprehensive solution
Teachers' Resources
Why do this problem?
This problem provides a visual context in which to consider how speed / time graphs represent movement over time. It allows opportunity for learners to discuss and refine their ideas. Asking learners to predict, to justify their predictions and to consider modifying their views can help address misconceptions and improve understanding. This problem could be used together with How far does it move?
Possible approach
With the dot in the centre, ask the group to predict what the path of the dot will be and what the speed-time graph will look like. Students could sketch the path and graph in advance, before seeing the polygon roll. Their suggestions could be compared and discussed before making a final joint judgement on the shapes of the path and the graph.
Run the interactivity. Discuss how the graph related to what students expected. Confirm understanding by asking what would happen if you changed the number of sides on the polygon.
At this point you might choose to do this card sorting activity which looks at all the possible positions for the starting point for the dot on a triangle. Can the students match the triangle with its corresponding graph and locus?
When the group feel confident, move them on to more challenging situations by moving the point to a vertex of other polygons (though note that the challenge set in the problem involves a pentagon with the dot in the middle of one side). Ask similar questions about the path of the dot and the speed-time graph.
Allow plenty of time for discussing/comparing different ideas before running the interactivity for the different polygon and point positions. The pause button is useful to focus on the different stages of the journey and to ask for conjectures about what will follow.
Ask pairs or groups to work on new questions, agreeing and drawing the graph and path together before using the interactivity to confirm their ideas.
Suitable questions are:
What happens if the dot is moved to a different vertex?
Key questions
- Why does the graph jump up or down (i.e. why are there discontinuities)?
- Why does the dot speed up and slow down at different stages of the "journeys"?
- If we change - (the polygon/position of dot) - what will be the same about the graph and what will be different?
Possible support
There are a number of variables affecting the speed/time graphs. Fix all but one of the variables and spend time making sense of the impact of that variable. For example, trying the dot at different vertices of a polygon, then looking at edges and interior points, before moving onto different polygons.
Possible extension
Pairs could draw out a speed-time graph they have generated and post it as a challenge for others to establish which initial settings were used(in the least number of guesses).
Students could create card sorting activities of their own.
The problem Up and Across develops this work further.
