Blackcurrantiest
Can you decide whose drink has the strongest blackcurrant flavour
from these pictures?
Problem
Image

Lizzie's Dad is making some blackcurrant squash for Lizzie and her friends.
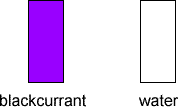
A purple rectangle stands for a measure of blackcurrant and a white rectangle for a measure of water:
Image
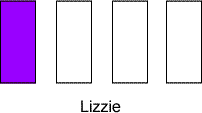
Can you decide which of these drinks, when mixed, will be the blackcurrantiest? (In other words, which one will have the strongest blackcurrant taste.)
Image

|
Image

|
|
Image

|
Image
|
Order the drinks from the blackcurrantiest to the one which would have the least blackcurrant flavour.
Can you explain why you have put them in that order?
Getting Started
Whose drink has most blackcurrant flavour, Imran's or Ambreen's?
Whose drink has most blackcurrant flavour, Ambreen's or Lizzie's?
Whose drink has most blackcurrant flavour, Francis' or Ambreen's?
Whose drink has most blackcurrant flavour, Imran's or Francis'?
Student Solutions
We received many well explained solutions to this problem. Martha from Baines Endowed C of E Primary School says:
Francis has the blackcurrantiest drink because he has two blackcurrants and one water.
Imran has the next blackcurrantiest drink because he has one blackcurrant and one water.
Ambreen has the second weakest blackcurrant because she has one blackcurrant and two waters.
Lizzie has the weakest blackcurrant because she has one blackcurrant and three waters.
You're right, Martha, well done, but I wonder if you could explain a bit more about how you compared the drinks? Boyang from Mountfields Lodge told us:
If Ambreen's drink has $2$ water and 1 blackcurrant, $\frac{1}{3}$ of her drink is blackcurrant.
If Francis' drink is $1$ water and $2$ blackcurrant, $\frac{2}{3}$ of his drink is blackcurrant.
If Imran's drink is $1$ water and $1$ blackcurrant, $\frac{1}{2}$ of his drink is blackcurrant.
If Lizzie's drink is $3$ water and $1$ blackcurrant, $\frac{1}{4}$ of her drink is blackcurrant.
Ambreen is A
Francis is F
Imran is I
Lizzie is L
I's drink is $\frac{6}{12}$ blackcurrant.
A's drink is $\frac{4}{12}$ blackcurrant.
F's drink is $\frac{8}{12}$ blackcurrant.
L's drink is $\frac{3}{12}$ blackcurrant.
F has the most blackcurrant so Francis' drink is the blackcurrantiest.
Pupils from Jebel Ali School, Dubai added to this by concluding that Francis had the blackcurrantiest drink, Imran was next, Ambreen's was after Imran and Lizzie had the least blackcurrant flavour.
Teachers' Resources
Why do this problem?
The pictorial aspect to this problem makes the concept of proportion easier to grasp. Moreover, this is a good context for encouraging children to explain their answers fully.
Possible approach
An appealing way to introduce this problem might be to make up a glass of fruit drink with the children, deliberately using one measure of water to one measure of concentrate. Invite the children to suggest what you would need to change in order to make the drink taste more or less 'blackcurranty'. Make sure the group realises that either the amount of blackcurrant or the amount of water
could be altered. In this practical context, you could compare the colour of the drinks too as a check.
From the practical, move on to introduce the class to the rectangle representation. Starting with one rectangle of blackcurrant and one of water, you could ask how the drink could be made less/more blackcurranty. Listen out for learners who justify their solution with reference to proportion. Some might talk about having more or fewer blackcurrant rectangles with the same number of water
rectangles. Some might use fractions to describe the proportion, for example that one part blackcurrant with two parts water means that the proportion of blackcurrant is $\frac{1}{3}$. You could use this problem as a way of introducing this kind of notation.
Once the class has worked on the problem itself in pairs, you could try out their ideas practically using fruit drink.
Key questions
Looking at these two drinks, which has most blackcurrant flavour?
How do you know?
Possible extension
Some children could be challenged to draw rectangles which represent other drinks according to certain criteria. For example, can they draw drinks that would be placed between each of the four children's drinks in the order of strength?
Possible support
Give children the opportunity to talk to a partner about this activity so that they are not worried about using precise vocabulary at first. Describing the proportion of blackcurrant in each drink in terms of a fraction will help the comparisons.
