W Mates
Show there are exactly 12 magic labellings of the Magic W using the
numbers 1 to 9. Prove that for every labelling with a magic total T
there is a corresponding labelling with a magic total 30-T.
Problem
Here is one of the magic labellings of the W shape from Magic W problem with a magic total of $14$ on each of the four lines making the W shape.
Image
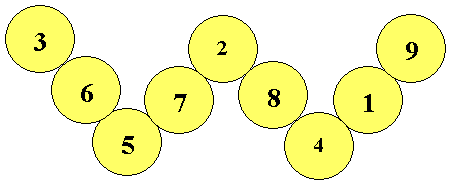
Prove that for every labelling with a magic total $T$ there is a corresponding labelling with a magic total $30-T$.
Find the values of $T$ for which magic labellings exist and show that there are a total of $12$ magic labellings altogether.
Note that two labellings are considered to be the same if they are reflections of each other or if the two numbers at the ends of the outside legs are interchanged.
Getting Started
Replacing the sequence of natural numbers $n$ from $1$ to $9$ by the numbers $10-n$ gives the numbers $1$ to $9$ in reversed order
Student Solutions
Thank you for your solutions to John from State College Area High School, Pennsylvania, USA, Andrei Lazanu from School No. 205, Bucharest, Romania, Sarah from Madras College St Andrew's Scotland and Patrick and his friend David Lee Yick Ming from Hkma David Li Kwok Po College, Hong Kong. This is John's solution.
First, I show that for every solution with a magic total $T$ there is a corresponding solution with magic total $30-T$. Consider what would happen if every element $x$ in a solution were replaced with the element $10-x$. All elements from $0$-$9$ would still be used, and all of the rows would have a sum $30$ minus the original total. Since all the row-sums were initially equal, they would still be, but each sum would be $30$ minus the old one, that is $30-T$.
Now I'll find all possible magic arrangements. First, I'll introduce my notation. Call the top centre vertex (occupied by the $2$ in the example picture) $a$. Call the lower left one $b$ (currently $5$). Call the lower right one ($4$) $c$. Arbitrarily, I'll set $b> c$, since solutions that are reflections of each other are considered to be identical.
Now, it is clear that the sum of the totals of all four rows will be equal to $(1+2+3+4+5+6+7+8+9)+a+b+c$, since $a,\ b$, and $c$ are the only elements to appear in all four rows. This simplifies to $45+a+b+c$. If all four rows are equal, the magic total, in terms of $a,\ b$, and $c$, will be $(45+a+b+c)/4$ since there are four rows. For the magic sum to be integral, $(a+b+c)$ must be one less than a multiple of 4. Possible sums for $a+b+c$ are then $3$ ($T=12$), $7$ ($T=13$), $11$ ($T=14$), and $15$ ($T=15$). We need not consider any arrangements with $T> 15$, as they would have corresponding arrangements with $T< 15 $as discussed in the first paragraph. We may also ignore $a+b+c=3$ as values that small cannot be chosen from the integers $1$ through $9$. The possible sums $a+b+c$ are therefore 7, 11, and 15, with $T=13,\ 14$, and $15$ respectively.
We may further narrow the search by eliminating the case $a+b+c=15$. When $a+b+c=15$, the magic sum $T$ also =15. Since $a$ and $b$ appear together in one row, the other number needed to give a sum of 15 in that row is $c$. However $c$ cannot appear in that row as it must appear elsewhere. Therefore $a+b+c=7$ or $11$. Now I'll use a brute force search to find all solutions. All possible arrangements are listed below. I checked each of them to determine if it yielded a Magic W. Those that did have the numbers listed as they appear from left to right in the W. Those that did not are marked only with an 'X'.
For $a+b+c=7,\ T=13$
\begin{eqnarray} % the * suppresses equation
numbering (a,b,c)&= \\ % & is the column separator
(4,2,1)&\rightarrow &562748139 \\ (2,4,1)&\rightarrow
&X \\ (1,4,2)&\rightarrow &X.\\ \end{eqnarray}
For $a+b+c=11,\ T=14$
\begin{eqnarray} (a,b,c)= \\ (8,2,1)\rightarrow
392485167 \\ (7,3,1)\rightarrow 293476158 \\ (6,3,2)\rightarrow X,\
(6,4,1)\rightarrow X,\ (5,4,2)\rightarrow X \\ (4,6,1)\rightarrow
X,\ (4,5,2)\rightarrow X,\ (3,7,1)\rightarrow X \\
(3,6,2)\rightarrow 176539248 \\ (2,8,1)\rightarrow X,\
(2,6,3)\rightarrow X \\ (2,5,4)\rightarrow 365728419 \\
(1,8,2)\rightarrow X \ (1,7,3)\rightarrow X \\ (1,6,4)\rightarrow
356719428. \\ \end{eqnarray}
There are $6$ solutions with $T< 15$, and therefore $6$
corresponding ones with $T> 15$, for a total of twelve. All are
listed below:$T=13$ $562748139$
$T=14$ $392485167$, $293476158$, $176539248$, $365728419$, $356719428$
$T=16$ $718625943$, $817634952$, $934571862$, $745382691$, $754391682$
$T=17$ $548362971$
