Escriptions
For any right-angled triangle find the radii of the three escribed
circles touching the sides of the triangle externally.
Problem
The idea for this problem was suggested by Geoff Faux. See also the NRICH Problem 'Polycircles' .
|
Try to visualise necklaces of touching circles centred at the
vertices of a right-angled triangle, first where the circles touch
on the sides of the triangle and then where points of contact lie
on the sides produced. Now try to visualise where these circles
meet the inscribed and escribed circles of the triangle.
Given any right-angled triangle $ABC$ with sides $a, b$ and
$c$, find the radii of the three circles with centres at $A, B$ and
$C$ such that each circle touches the other two and two of the
circles touch on $AB$ between $A$ and $B$, two circles touch on
$CA$ produced and two circles touch on $CB$ produced.
Now for any right-angled triangle $ABC$ find the radii of the
three escribed circles as shown in the diagram.
|
Image
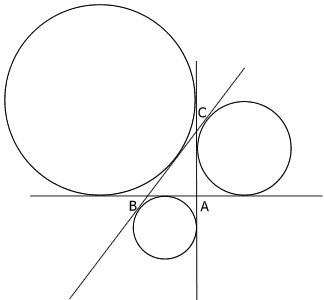
|
Getting Started
The critical idea here is that radii and tangents to circles meet
at right angles. Look for squares.
Student Solutions
This question uses the same method as the problem Polycircles from February 2000 and you might find it helpful to experiment with the interactive diagram.
The best solution to this problem came from Andrei Lazanu, age
13 of School No. 205, Bucharest, Romania. Can you finish off the
solution?
I drew a right angled triangle, and circles having as centres
the vertices of the triangle, and being tangent two by two at
points on the sides of the triangle.
Let $r_A,\ r_B$ and $r_C$ be the radii of the touching circles
centred at the vertices of the right angled triangle ABC, of sides
$a,\ b$ and $c$, with the centres at the points A, B and C
respectively. These radii satisfy the conditions:
$$\eqalign{ r_A + r_B &= c \cr r_B + r_C &= a \cr r_C
+ r_A &= b.}$$
This system of three equations with three unknowns could be
solved in the following manner: adding all three equations,
dividing the result by two and subtracting one by one the
equations. I obtained:
$$\eqalign{ r_A &= {1\over 2}(b+c-a) \cr r_B &=
{1\over 2}(a + c - b) \cr r_C &= {1\over 2}(a + b - c)
\cr.}$$
I also drew the three escribed circles, as well as their
points of intersection. I see that on each side, the points of
intersection of the circles with centres at the vertices are the
same as the points of tangency of the escribed circles with the
sides. This can be explained by the fact that the lengths of the
tangents to a circle, drawn from a point exterior to the circle,
have equal lengths. This will enable us to find the radius of an
escribed circle.
Image
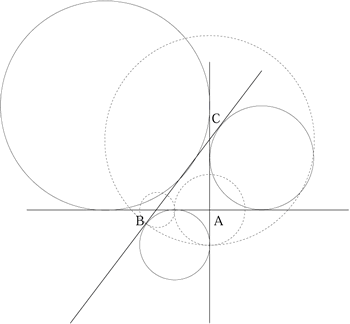
Given any right angled triangle $ABC$ with sides $a,\ b$ and
$c$, we have to find the radii of the three circles shown in the
diagram with centres at $A,\ B$ and $C$ such that each circle
touches the other two and two of the circles touch on $AB$ between
$A$ and $B$, two circles touch on $CA$ produced and two circles
touch on $CB$ produced.
The method is exactly as above but here we have
$$\eqalign{r_A + r_B &= c \cr r_C - r_A &= b\cr r_C -
r_B &= a.}$$
By solving these equations and identifying which circles have
equal radii you should be able to find the radius of one of the
escribed circles.
The radii of the other escribed circles are found
similarly.
