Problem | Teachers' Notes | Hint | Solution | Printable page |

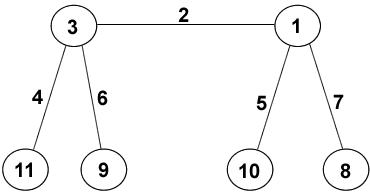
In the Land of Trees all the caterpillars have numbers on their feet and hips (vertices) and on their legs and body segments (edges) as shown on this 4 legged caterpillar. All the whole numbers from 1 to $v+e$ are used where $v$ is the number of vertices and $e$ is the number of edges. Biologists classify them by their vertex-sums. A vertex sum is the total of the numbers on the vertex and all the edges at that vertex. The caterpillar shown has vertex sums: 11,13,15,17,25,30.

Show that one day a biologist may find a rare magic 4-legged caterpillar having the same sum at all its vertices and describe this creature. Could there be two species of magic 4-legged caterpillars with different numberings? Prove that no matter how long they search it will be impossible to find any magic 6-legged caterpillars. What about magic caterpillars with even more legs?

Logo. Factors and multiples. Mathematical reasoning & proof. Networks/Graph Theory. Simultaneous equations. Combinatorics. Games. Manipulating algebraic expressions/formulae. Working systematically. Creating expressions/formulae.