Cocked Hat
Sketch the graphs for this implicitly defined family of functions.
Problem
The implicit equation
$$(x^2 + 2a y -a^2)^2 = y^2(a^2 - x^2)$$
represents a family of functions the members of the family corresponding to different values of $a$.
Re-arrange the equation into the form $y= f(x)$ and draw some graphs belonging to the family for different values of $a$. What is the domain of the function $f(x)$?
To investigate these graphs you might try http://www.desmos.com.
Getting Started
Expand the square the left hand side of the expression and rearrange the expression to give a quadratic equation in $y$. Now solve the quadratic equation. This will give two solutions (as quadratic equations generally do) and each will give you the equation of a branch of the graph. Sketch the graph by considering where real values of $y$ exist, where the graph crosses the axes and what symmetries it has. You can use graphing software but it is much more of a challenge to sketch the graph without.
Don't let this defeat you. It is not nearly as hard as it looks but you have to do a little algebra. If you wish you can choose a particular value for $a$, say $a=1$, and investigate one member of the family of graphs but then you will have to go back and see what happens for different values of $a$. You can use graphing software but it is much more of a challenge to sketch the graph without.
Student Solutions
| Congratulations Aleksander from Gdynia Bilingual High School No3, Poland for your excellent solution to the Cocked Hat problem. As you will see, the solution hinges on simplification of an algebraic expression and solving a quadratic equation. |
Here is Aleksander's
solution.
First we will rearrange the expression from implicit to
explicit form. The given equation is
$$(x^2 + 2ay -a^2)^2 = y^2(a^2 - x^2)$$
Squaring the LHS gives
$$4a^2y^2 + 4ay(x^2-a^2) + (x^2 - a^2)^2 = y^2(a^2 -
x^2).$$
Collecting like terms gives the quadratic equation
$$y^2(3a^2+x^2)+ 4ay(x^2-a^2) + (x^2 - a^2)^2 = 0.$$
The discriminant is
$$\Delta = {16a^2(x^2 - a^2)^2-4(3a^2+x^2)(x^2-a^2)^2}= (x^2 -
a^2)^2(4a^2-x^2) = 4(a^2 - x^2)^3.$$
Solving this equation we get:
$$\eqalign{ y &= {-4a(x^2 - a^2)\pm \sqrt{4(a^2 -
x^2)^3}\over 2(3a^2+x^2)} \cr &= {(x^2-a^2)(-2a\pm
\sqrt{(a^2-x^2)})\over (3a^2+x^2)} }$$
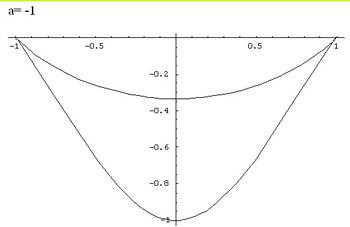
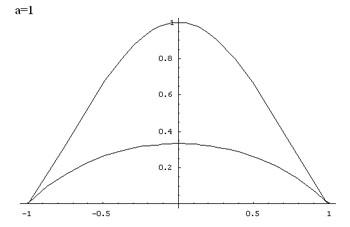
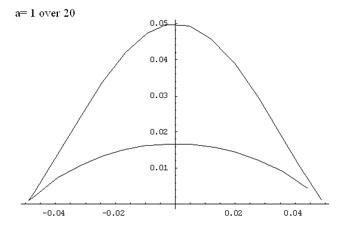
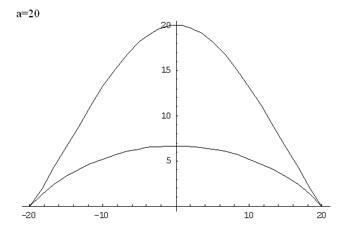
For each value of $a$ there are two branches of the graph
given by taking the +ve and -ve signs in this equation. Values of
$y$ are only defined for the interval $-a \leq x \leq a$. The
domain of $f(x)$ is $-a \leq x \leq a.$ The zeros of the function
are given by $x = a$ and $x = -a.$
Additionally, the function is symmetric with respect to the
y-axis, because $x$ always appears in even powers. Graphs for
parameters $a = n$ and $a = -n$ and are symmetric to each other
with respect to the x-axis, that is $y(n) = y(-n)$. Proof:
$$ {(x^2-n^2)(-2n\pm \sqrt{(n^2-x^2)})\over (3n^2+x^2)} =
-{(x^2-(-n)^2)(-2(-n)\pm \sqrt{(-(n)^2-x^2)})\over
(3(-n)^2+x^2)}$$
Here are some graphs of the function:
Image
|
Image
|
Image
|
Image
|
