Magazines
Let's suppose that you are going to have a magazine which has 16 pages of A5 size. Can you find some different ways to make these pages? Investigate the pattern for each if you number the pages.
Problem
Sometimes in organisations or clubs people like to make a small magazine. Perhaps you belong to a club or a group, and if you can use the photocopier it's maybe cheaper than using the computer printer.
So let's suppose that you are going to have 16 pages of A5 size, which you can get by using both sides of A3, [which is twice as big as your usual A4] and folding it in half three times. That is halve it, halve it again and finally halve that again.
I've discovered so far four ways of doing this but I guess there are more.
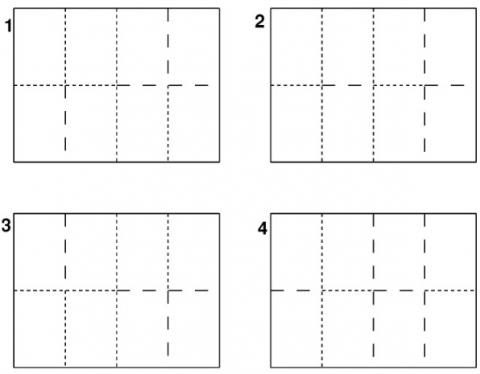
I've used small dotted lines to show 'valley' folds and large dashed lines to show 'mountain' folds.
Number 1 came by doing:- Right over Left; Bottom over Top; Left over Right.
Number 2 came by doing:- Right over Left; Right over Left; Bottom over Top.
Number 3 came by doing:- Right over Left; Bottom over Top; Right under Left.
Number 4 came by doing:- Right over Left; Right over Left; Bottom under Top.
Try these for yourself and see what others you can come up with.
Well that may be enough of an investigation for you and you might like to think about what happens when you do only two halvings [for an 8-page magazine] or four halvings [for a 32-page magazine]!
But those of you who wish to stick to the A3 [being halved three times] and 16 pages being stuck to both sides of the A3 ready for photocopying, let's have a look at the numbering of the pages. So that when you cut up all the folds except the centre one you are ready for stapling.
Here's what I found I had to do to get the numbering correct. Number 1 shows the front and then number 2 shows it turned over.
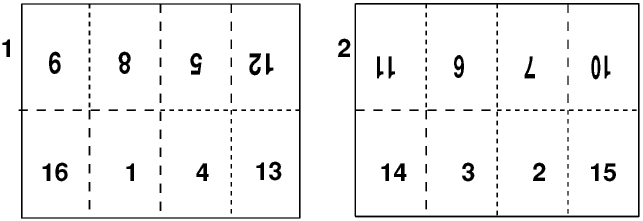
Try and number the pages for one of your foldings that was different from mine and see what you get. It's probably different, I would think it would be. I'm not quite sure about the stapling either?
These 16 numbers looked interesting so I've separated them from the drawing.
| 9 | 8 | 5 | 12 | |
| 16 | 1 | 4 | 13 | |
| 11 | 6 | 7 | 10 | |
| 14 | 3 | 2 | 15 |
I put the 'reverse side' numbers underneath.
Whoa! Left-hand pairs make 17 and so do the right-hand pairs!
I expect there's a lot more to see here.
Well have a go, and don't forget to say every now and again, "I wonder what would happen if I ...?''.
Getting Started
Having some sheets of paper to fold and write on will be a great help.
Student Solutions
We haven't received any solutions to this problem and of course what you find out might depend on what you decided to investigate.
However, we would love to hear about anything you have discovered. Share your ideas by emailing primary.nrich@maths.org Please don't worry that your solution is not "complete" - we'd like to hear about anything you have tried. Teachers - you might like to send in a summary of your children's work.
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
For more extension work
Possible support
