Tetra Inequalities
Can you prove that in every tetrahedron there is a vertex where the three edges meeting at that vertex have lengths which could be the sides of a triangle?
Problem
Consider a tetrahedron $ABCD$.
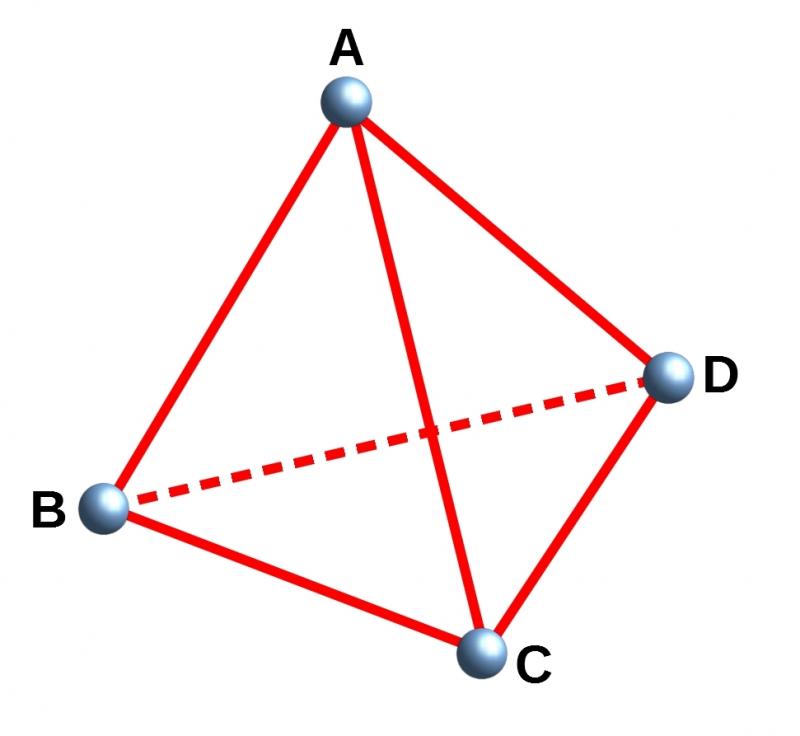
Can you prove that in every tetrahedron there is a vertex where the three edges meeting at that vertex have lengths which could be the lengths of the sides of a triangle?
Have a think about the problem first, and then below there are some hints and suggestions that might be useful.
---------------------------------------------------------------------------
What does this problem mean? Can you rewrite it in a different way?
Show alternative
If we consider the point $A$, then there are three edges that meet this, $AB$, $AC$ and $AD$. These three lengths might, or might not, be possible lengths of the sides of a triangle.
The problem is asking you to prove that in every tetrahedron there exists at least one vertex where the three edges meeting this vertex have lengths which could be the lengths of the sides of a triangle.
Alternatively, this problem is asking you to show that it is impossible to have a tetrahedron where none of the vertices have three edges whose lengths cannot be the lengths of the sides of a triangle.
You could try sketching some tetrahedrons to get a "feel" for the problem.
What does it mean that three lengths can be the sides of a triangle?
Which of the following sets of lengths could be the lengths of the sides of a triangle?
- 5, 5, 8
- 5, 5, 12
- 3, 4, 5
- 3, 4, 7
If a triangle has lengths $a, b, c$ where $a \le b \le c$, can you write down an inequality connecting $a, b$ and $c$?
Show inequality
If the three lengths can form a triangle, then the longest one must be less than the sum of the two shorter sides. We can write this as $a+b > c$. In the case $a+b=c$ then the sides could be thought of forming a triangle with zero area, but for the purposes of this problem we will consider this to not be a triangle.
Note that we are not being asked to show that every vertex in a tetrahedron has three edges meeting it which could be the sides of a triangle. Can you sketch out a tetrahedron where one vertex has three edges meeting it which are not a possible sets of sides of a triangle? Click the button below to see our attempt:
Show tetrahedron
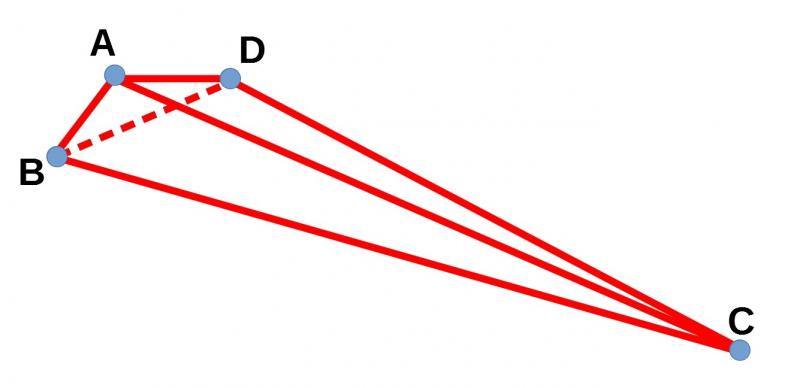
In this tetrahedron we have $|AB|+|BD|<|BC|$, so the three edges meeting at $B$ cannot be the sides of a triangle. However, it does look like the three edges meeting at $C$ could be the sides of a triangle.
To try and prove the statement, we can start by assuming that there exists a tetrahedron in which none of the vertices has three edges which could be sides of a triangle. We can then try and show that this leads to a contradiction (or in other words, that this tetrahedron is impossible).
WLOG (Without Loss of Generality) let the longest edge of the tetrahedron be the edge $AB$. (It doesn't really matter which side the longest edge is, and we can relabel the vertices so that $AB$ is the longest). Here are a few questions to consider, bearing in mind that we have assumed that in our tetrahedron there is no vertex where the three edges that meet it have lengths which could be the sides of a triangle.
- Can all of the six edges be the same length?
- Can five of the edges be the same and then the last one is smaller?
- Can four/three/two lengths be joint longest?
Show answers
If all of the lengths are the same then all three edges meeting any vertex are the same, and so can form an equilateral triangle.
If three of more edges are "joint longest" then there will be at least one vertex where two of these edges meet. Then these two edges and the third form an isosceles triangle.
It is possible to have two "joint longest" edges, as shown in the diagram below:
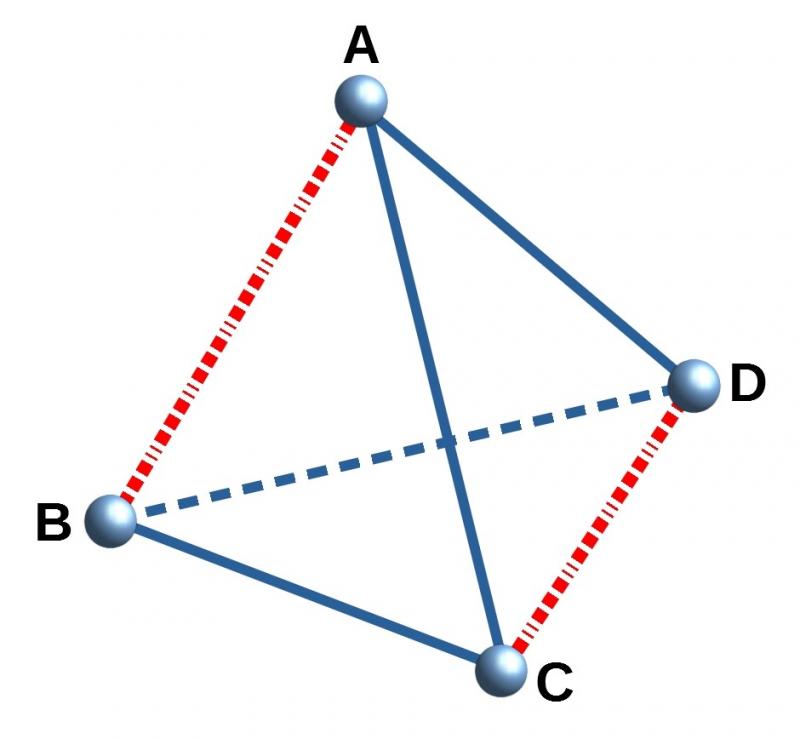
Assuming that $AB$ is the longest side (we might have $AB=CD$), and that the three edges meeting at $A$ have lengths which cannot be the sides of a triangle, can you write down an inequality for the lengths of these edges? Can you write down an inequality involving the three edges meeting at $B$?
Show inequality
If the three lengths do not form a triangle then we have $AB \ge AC + AD$.
Noting that the face $ABC$ is a triangle, can you write down an inequality involving these three edges? Can you find a similar inequality for face $ABD$?
Can you arrange the two pairs of inequalities in such a way that they contradict each other?
You should find that you have two inequalities which form a contradiction. This means that the original assumption that there exists a tetrahedron in which none of the vertices has three edges which could be sides of a triangle. Therefore every tetrahedron has three edges meeting at a vertex whose lengths could form the sides of a triangle.
Getting Started
There are lots of hints in the problem to help you.
To help you understand the problem, you can start by working out some sets of lengths which can, or cannot be the lengths of the sides of a triangle. This should lead you to the Triangle Inequality which states a relationship between the longest side of the triangle and the two shorter ones which must be true if the lengths are the lengths of the sides of a triangle.
Try sketching a tetrahedron where none of the vertices have three edges whose lengths could be the lengths of the sides of a triangle. Can it be done? You could assume that such a tetrahedron exists, and then show that this is actually impossible (called a proof by contradiction).
Student Solutions
Well done to Gabriel from London Academy of Excellence Tottenham and Ruth from Manchester High School for Girls who solved this problem correctly. Gabriel sent in a long exploration and Ruth sent in a short proof. Here, Gabriel's exploration is shown first and Ruth's proof is shown below.
First, Gabriel explored the properties of triangles, and what it means if three lengths 'could be the sides of a triangle' (click to enlarge):

Next, Gabriel applied these ideas to a tetrahedron, and assumed that none of the vertices are joined to three edges which could be the sides of a triangle (click to enlarge):

Gabriel then made another assumption, which allowed the proof to be completed:

It was fair for Gabriel to assume that $a$ was the longest side, because at that point there was nothing to differentiate between the sides - any of them could have been called $a,$ so we can choose that $a$ is the longest side.
Once $a$ is the longest side, there is now a diffrerence between the other sides: they either share an edge with $a$ (ie $b,c,d$ or $e$) or they do not share an edge with $a$ (ie $f$). Gabriel has proved that if $f$ is the second-longest side, then the tetrahedron is impossible. What if $b,c,d$ or $e$ is the second longest side?
Here is Ruth's proof that in every tetrahedron there is a vertex where the three edges meeting at that vertex have lengths which could be the lengths of the sides of a triangle:
The tetrahedron's vertexes are $A, B, C$ and $D$ and the longest side is $AB.$
If you assume that there is not a vertex where the three sides meeting at it could be the sides of a triangle,
$AB + \text{either of the other sides at }A\text{ or }B \gt \text{the third side at that vertex}$
$\therefore AC + AD \lt AB$ and $BC + BD \lt AB,$ otherwise the sides meeting at $A$ or $B$ could be the sides of a triangle.
$\therefore AC + AD + BC + BD \lt 2AB\hspace{6mm}(1)$
$ABC$ and $ABD$ are both triangles
$\therefore AC + BC \gt AB$ and $AD + BD \gt AB$
$\therefore AC + AD + BC + BD \gt 2AB\hspace{6mm}(2)$
$(1)$ and $(2)$ are contradictions
$\therefore$ the initial assumption is wrong
$\therefore$ there is at least one vertex where the three sides meeting at it could be the sides of a triangle.
Can you represent the triangle inequality using a diagram? Can you explain Ruth's proof using a diagram?
Teachers' Resources
Why do this problem?
This problem uses proof by contradiction to prove that a statement is true. Students will be required to think about inequalities (which they can often find difficult), and will need to construct a clear logical argument.
Key Questions
- Can you write down the lengths of some possible triangles?
- Can you write down three lengths which cannot be the lengths of the triangle?
- If a triangle has lengths $a, b$ and $c$, what inequality must the lengths satisfy?
- If $p>q$ and $r>s$, what can you say about $p+r$?
The problem Tetrahedron Tester could be used as an introduction to the triangle inequality.
