Same Length Trains
How many trains can you make which are the same length as Matt's and Katie's, using rods that are identical?
Problem
Same Length Trains printable sheet
Matt and Katie were using Cuisenaire rods. They placed rods end to end to make 'trains'.
Here are their two trains:

What is the same about the two trains?
What is different?
You might have noticed:
- the trains are the same length as each other
- the top train uses rods that are all different (light green, black, pink and dark green)
- the bottom train uses rods that are all the same (white)
- there are four rods in the top train
- there are 20 rods in the bottom train
- the white rods are the shortest
- the white rods are all the same length
- each colour rod is a different length
Can you make some more trains the same length as Matt's and Katie's trains, each using rods of just one colour?
How many different trains can you make?
How do you know you have found all the possible trains?
If you haven't got any Cuisenaire rods, you may like to use the interactivity below to try out your ideas.
You may be interested in the other problems in our Cuisenaire Feature.
Getting Started
How will you record what you have done?
How will you know that you have found them all?
How many white rods are used in the train in the picture? How might that help?
Student Solutions
We had just a few solutions sent in for this task and here you can see a progression of ideas in the solutions.
Eva from Elmgrove School sent in the following:
I noticed that the white train contained 20 rods. Both of the trains were the same length, but consisted of different numbers of each rod. There were different colours rods. What also caught my eye was that the different colour train's rods were not the same size.
Hebey from Venkateshwar International School in India sent in this image:

Luay from Goldsworth Primary School sent in the following image:

Simran from Maurice Hawk School in the USA sent in a Word document as follows:
First, I noticed that if I arrange all the rods from smallest to largest, each rod is 1 unit longer than the previous rod (please see picture).
w= 1 unit, r= 2, g= 3, p= 4, y= 5, d= 6, b= 7, t= 8, B= 9 and o= 10
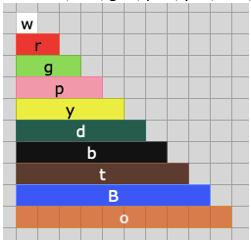
The train shown in this picture is made of 20 white rods. To find out which other colour rods can make this train, I decided to skip-count. If you reach 20 using skip-counting, then that colour rod can be used to make the train. The number of times you skip-count tells you how many rods you need to use to make the train.
r (2 units long) = 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 (10 red rods are needed to make the train)
g (3 units long) =3 , 6, 9, 12, 15, 18, 21 (You cannot use the green rod because you don't get 20 during the skip-count, you can make a train that is 18 units long or 21 units long but not 20 units long)
p (4 units long) = 4, 8, 12, 16, 20 (5 pink rods are needed to make the train)
y (5 units long) = 5, 10, 15, 20 (4 yellow rods are needed to make the train)
d (6 units long) = 6, 12, 18, 24 (Cannot use dark green rods)
b (7 units long) = 7, 14, 21 (Cannot use black rods)
t (8 units long) = 8, 16, 24 (Cannot use tan rods)
B (9 units long) = 9, 18, 27 (Cannot use blue rods)
o (10 units long) = 10, 20 (2 orange rods are needed to make the train)
Red, pink, yellow and orange rods can be used to make the train. When I solved this problem, my brother told me that you can find the factors of 20, which are numbers that can be multiplied to make 20. So, 1, 2, 4, 5 and 10 are factors of 20. By using this strategy, again, red, pink, yellow and orange rods can be used to make the train.

Well done to those of you whose work we've seen. We hope to hear from you again in the future!
Teachers' Resources
Why do this problem?
Possible approach
Introduce the task by telling the 'story' of Matt and Katie creating 'trains'. Show the picture of their two trains and invite children to talk in pairs about what is the same and what is different about them. After a short time, draw the whole group together and share their noticings, writing them up on the board for all to see. Encourage everyone to comment on these noticings, rather than you being the one to answer questions or validate the contributions. Having listened to the class' observations, you may wish to reveal the bullet points in the problem too.
You can then introduce Cuisenaire rods and set up the task for children to work on in pairs, either using real rods or the interactivity on a tablet or computer. As they work, look out for the different ways that they are approaching the task. Some children might be choosing a rod at random to see whether it works, others may decide to start with the next shortest rod (red), or the longest rod (orange) and work up/down in order. You could bring everyone together for a mini plenary to share your observations and to encourage systematic working. Remember that there are lots of ways to work systematically, so try to take time to understand a pair's system, even if it is one that you wouldn't choose to adopt.
You may like to make an area of the board or wall or flipchart available for children to come up and record when they have found a train that works, or have the interactivity on the whiteboard so that they can create a train for all to see. Encourage the rest of the class to be checking the solutions that are put up, rather than you yourself being the 'checker'. In the plenary, you could use the solutions that have been contributed by the class to model one way of working systematically (or ask a pair to share their way) and that will help reveal whether all the possible solutions have been found, or not.
If you are keen to use this as an opportunity to focus on factors and multiples, look out for pairs who are working in a numerical way and share their approach. Alternatively, you could draw attention to the numerical representation of the rods by reminding the class, or asking them, how many white rods were used in the pictured train. If we say a white rod is 1 unit long, how long are the other rods, comparing them to white? What colour trains have the children been able to make that are 20 white rods long? Why has no-one been able to make a train which is made only of light green rods, for example?
Key questions
How will you remember your solutions?
How can you record what you have done?
Possible support
Try to offer real Cuisenaire rods if at all possible, otherwise invite pairs of children to use the interactivity on a tablet or computer. Some children might find it helpful to record on squared paper.
Possible extension
Learners could try using different numbers of white rods to make 'same length trains' with rods of just one colour. Using 21, 22, 23 and 24 could prove interesting. When is it impossible to make trains using rods of just one colour other than white?
In addition, children might like to investigate making some 'same length trains' using rods of all different colours.
