Cosy Corner
Six balls are shaken. You win if at least one red ball ends in a corner. What is the probability of winning?
Problem
Cosy Corner printable sheet - problem
Cosy Corner printable sheet - recording sheet
A container holds $3$ red balls, $2$ blue balls and $1$ yellow ball.
The balls are identical in all ways except colour.
Shake the container, and look at how the balls settle in the triangle.
You win if at least one of the red balls is in a corner.
Did you win?
Complete several shakes and look at your results.
Approximately how often do you think you would win if you completed $100$ shakes?
Make a prediction and then check it by doing the experiment.
Can you find a way of working out the theoretical probability of winning?
You may find this Recording Sheet useful.
Getting Started
In how many different positions can the three red balls settle?
How many of these positions contain no red balls in a corner?
You may find this Recording Sheet useful.
Student Solutions
Ruby and Emma from Yewdale Primary in England used the interactivity to estimate the chance of winning:
For our working out we decided to look at how many wins we got out of 1000
instead of 100.
100: 93 0.930
100: 92 0.920
100: 97 0.970
100: 95 0.950
100: 93 0.930
100: 97 0.970
100: 98 0.980
100: 93 0.930
100: 93 0.930
100: 95 0.950
Daniel from Bayside School in Gibraltar and Sanika P from PSBBMS, OMR in India used probability directly. This is Daniel's work:
There are 6 positions that a ball can take, and out of those 6, 3 are corners.
To lose, you must end up with no red ball in a corner, and for that to happen, the 3 non corner spaces must each be taken up by a red ball.
For 1 red ball to take up a non corner space, the probability is $\frac36$
Given that one red ball is in a non corner position, the probability that the next red ball ends up in a non corner position is $\frac25$, and given that the two red balls are in central positions, the probability that the next red ball does not end up in a corner is $\frac14$.
The probability of no red ball landing in a corner spot is $\frac36\times\frac25\times\frac14$ which is $\frac1{20}$.
So the probability that a red ball does land in a corner is $1-\frac1{20}=\frac{19}{20}=0.95$
Layla and Tamara from Frederick Irwin Anglican School in Australia counted the number of winning arrangements:
You want to start by deciding and experimenting with however many different possibilities there is for the red balls to settle in. To help with this we tried mirroring and reversing patterns to make more. We came up with the answer of 18 different positions. You must then figure out how many of those positions can no red balls be in the corners. The answer to that is only one position! So the formula would be approximately 1 in 18 tries that you would lose the game.

Layla and Tamara got 1 in 18 instead of 1 in 20 beacuse there are two arrangements missing:
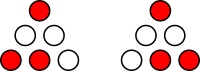
Using a systematic counting method like the one below can help us be sure there aren't any more missing:
red in 0 corners

1 arrangement
red in 1 corner

3 options for red corner, 3 options for which ? is not red:
9 arrangements
red in 2 corners

3 options for not red corner, 3 options for which ? is red:
9 arrangements
red in 3 corners

1 arrangement
Jacob from Acland Burghley in the UK used factorials:
I already know that to work out the number of ways of arranging a number of colours or in this case counters is the factorial of that number.
The factorial of $4$ is written $4!$ and means $4\times3\times2\times1$. There are $4!$ ways to arrange $4$ counters in $4$ spaces because:
There are $4$ empty spaces in which to place the first counter
For each of these $4$ options for the first counter, there will be $3$ options left for the second counter
For each of these $4\times3$ arrangements for the first two counters, there will be $2$ options left for the third counter, and only $1$ for the fourth.
The red tiles aren't interchangeable because when it is shuffling they are kept independent. With these two facts I know there are $720$ arrangements ($6!$).
The number of arrangements where you lose is $36$ because there are $6$ ways of arranging the $3$ reds that all need to be in the middle, and $6$ ways of arranging the outer counters in each way of arranging the middle ones, so $6\times6$ is how many ways to lose there are.
$720\div36=20$ so you lose $1$ in $20$.
Teachers' Resources
Why do this problem?
This problem offers an opportunity to explore and discuss two types of probability: experimental and theoretical. The simulation generates lots of experimental data quickly, freeing time to focus on predictions, analysis and justifications.
Possible approach
Demonstrate the interactivity a few times, explaining that to win, at least one corner needs to contain a red ball.
Invite students to estimate the probability of winning. Allow students some thinking and discussion time in pairs before bringing them together to state their initial conjectures.
Students may find this Recording Sheet useful, to work out the different possible outcomes.
Record their conjectures on the board and then run the interactivity a few hundred times. Then revisit students' conjectures and discuss which ones matched the experimental data, before rounding the activity off by discussing which methods for recording the different combinations were both successful and efficient.
Key questions
Are there efficient systems for recording the different possible combinations?
What counts as a different outcome?
If the red balls are in the same position but a blue and yellow ball swap places, does that count as a different outcome?
Possible support
An alternative problem for exploring theoretical and experimental probability is Flippin' Discs
Possible extension
A follow-up problem could be Two's Company
Teachers may want to use this recording tool to gather the results of other similar experiments that their students are carrying out:
