Retracircles
Four circles all touch each other and a circumscribing circle. Find
the ratios of the radii and prove that joining 3 centres gives a
3-4-5 triangle.
Problem
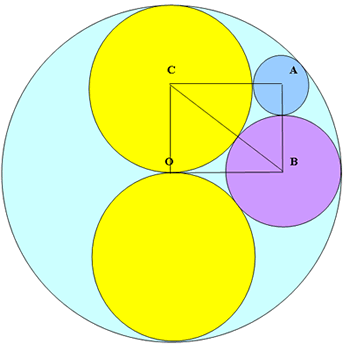
The circles centres $O$, $A$, $B$ and $C$ touch one another. Prove that the radii of the circles with centres $A$, $B$ and $C$ are in the ratio $1 : 2 : 3$ and that the triangles $OBC$ and $ABC$ are right angled $3 : 4 : 5$ triangles.
Image
Getting Started
$BO$ is a tangent to the two equal circles and hence angle $BOC$ is a right angle. If $OC=$3 units then the large outer circle has radius $6$ units. Pythagoras' theorem will give the radius of the circle centre $B$. You cannot assume that angle $BAC$ is a right angle.
Student Solutions
Image
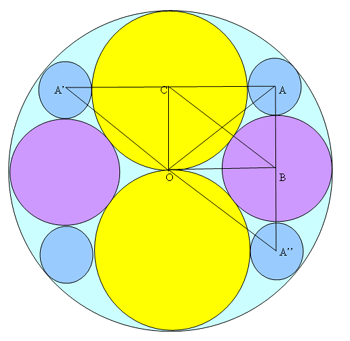
This solution is from Yatir Halevi.
Let $a$, $b$ and $c$ be the radii the circles centered at $A$, $B$ and $C$ respectively.
Angle $BOC = 90^\circ$ since, $OB$ is tangent to the circle centered at $C$ and hence it is perpendicular to the radius. That also means that the radius of the the circle centered at $O$ is $2c$.
As $BC$ connects $B$ and $C$ it is equal to $b+c$.
By Pythagoras theorem: $(2c-b)^2 + c^2 = (b+c)^2$. Hence $4c^2=6bc$ and $c$ can't be equal to $0$ so $2c=3b$.
We could extend the lines $AC$ and $BO$, to create a mirror image, where we have two circles centered at $A'$ and $B'$ with radii $a'$ and $b'$ respectively, and due to symmetry issues, $a'=a$ and $b'=b$. We will also connect $O$ with $A'$ and $O$ with $A$.
Now $OA=OA'= 2c-a$ and $AC = A'C = c+a$ and so the line $OC$ cuts $A'A$ in half, and because the sides of the triangle $A'OA$ are equal, $OC$ is also perpendicular to $A'A$, hence $\angle OCA = 90$.
As triangle $ACO$ is a right-angled triangle, using Pythagoras' Theorem: $AC^2+OC^2=AO^2$ and so $$(a+c)^2 + c^2 =(2c-a)^2$$ which simplifies to $6ac=2c^2$ and $c$ can't be equal to $0$ so $c=3a$. Combining this with $2c=3b$ we get: $3b=6a$ that is $b=2a$ and so $a=b/2=c/3$, that is they are in the ratio $1:2:3$ as required.
If we mirror the image in the line $BO$ thus creating a new circle below the one centered at $B$, centered at $A''$ it has the same radius as $A$ by symmetry. By the the same line of thought that we used before, we reach the conclusion that $\angle ABO=90$. What we get is that $CABO$ has 3 right angles, meaning that the fourth is also a right angle and that it is a rectangle and that triangle $ABC$ is also right angled.
Let's look at triangle $OBC$ in which $OB = 2c-b = 6a - 2a = 4a$, $OC = c = 3a$ and $BC = b + c = 2a+3a = 5a.$ So the ratio between the sides are $3:4:5$, like we wanted to prove.
Let's look at triangle $ABC$ in which $AB = a + b = a + 2a = 3a$, $AC = a + c = a + 3a = 4a$ and $CB = b + c = 2a + 3a = 5a$. So the ratio between the sides are $3:4:5$, like we wanted to prove.
Arun Iyer proved this result by applying Descartes Circle Theorem.
