Darts and Kites
Problem
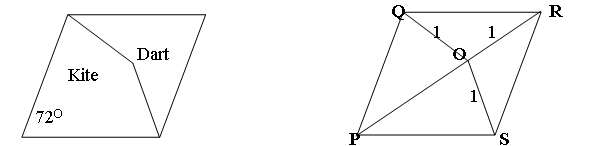
The diagram shows a rhombus $PQRS$ with an internal point $O$ such that $OQ = OR = OS = 1$ unit. Penrose used this rhombus, split into two quadrilaterals, a dart and a kite, to make his famous tiling which fills the plane but, unlike a tessellation, does not repeat itself by translation or rotation.
Find all the angles in the diagram, show that $POR$ is a straight line and show that triangles $PRS$ and $QRO$ are similar. Hence prove that the length of the side of the rhombus is equal to the Golden Ratio $(1+ \sqrt{5})/2$.
Getting Started
Use isosceles triangles, similar triangles and a quadratic equation.
Student Solutions
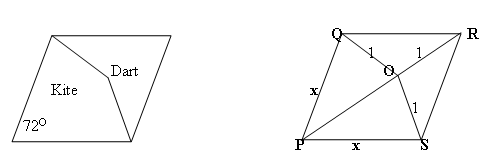
This solution is from Arun Iyer of SIA High School and Junior College.
Part 1
First I will show that $POR$ is a straight line. For this I would
like to state the perpendicular bisector theorem.
PERPENDICULAR BISECTOR THEOREM: Every point equidistant from the
two ends of a line segment lies on the perpendicular bisector of
the line segment.
Now consider the line segment $QS$.
$OQ=OS=1$ therefore by the perpendicular bisector theorem, $O$ must
lie on the perpendicular bisector of $QS$.
$PQ=PS$ (as the sides of the rhombus are equal), therefore by the
perpendicular bisector theorem, $P$ must lie on the perpendicular
bisector of $QS$.
$RQ=RS$ (as the sides of the rhombus are equal), therefore by the
perpendicular bisector theorem, $R$ must lie on the perpendicular
bisector of $QS$.
Now the perpendicular bisector of a line segment is unique and
hence $P$, $O$, $R$ must lie on the same perpendicular bisector and
hence $POR$ is a straight line.
Part 2
Now I will get all the angles of the rhombus.
$\angle QPS$ = $72^{\circ}$ (given), $\angle QRS = \angle QPS =
72^{\circ}$ as they are opposite angles of a rhombus. The diagonal
of the rhombus bisects the angles of a rhombus and therefore
$\angle QPO = \angle SPO = \angle QRO = \angle SRO =
36^{\circ}$.
Triangles $OQR$ and $OSR$ are isosceles triangles, therefore
$\angle OSR = \angle OQR = 36^{\circ}$.
Using the fact that sum of angles of a triangle is 180 degrees, we can see that $\angle SOR$ and $\angle QOR$ are equal to 108 degrees. Since we have proved that $POR$ is a straight line in Part 1, we can determine $\angle QOP$ and $\angle SOP$ to be 72 degrees.
Again using the fact that sum of angles of a triangle is 180 degrees, we can see that $\angle OQP$ and $\angle OSP$ are equal to 72 degrees.
Part 3
